Les formules de calcul de l'aire d'un triangle
Dans un contexte d'un triangle quelconque \(\{a, b, c\}\), avec chaque angle opposé respectivement à sa longueur, tel que :
$$ \left \{ \begin{gather*}
\alpha \enspace opposé \enspace à \enspace a \\
\beta \enspace opposé \enspace à \enspace b \\
\gamma \enspace opposé \enspace à \enspace c \end{gather*} \right \} $$
Et tel que la figure suivante :
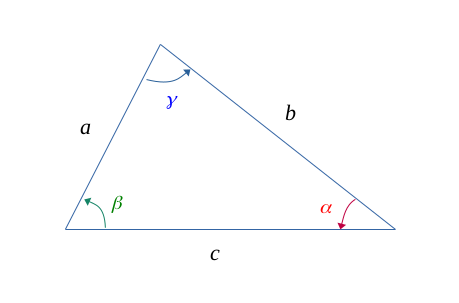
Formule de l'aire
La fomule de l'aire nous dit que :
$$\forall (a, b, c) \in \hspace{0.05em} \mathbb{R}^3, \enspace (\alpha, \beta, \gamma) \in \hspace{0.05em} \mathbb{R}^3, $$
Formule de Héron
La fomule de Héron nous dit que :
$$\forall (a, b, c) \in \hspace{0.05em} \mathbb{R}^3,$$
$$ S_{abc} = \sqrt{p(p-a)(p-b)(p-c)} \qquad (Héron) $$
$$ avec \enspace \Biggl \{ \begin{gather*}
p : demi\hspace{-0.3em}-\hspace{-0.3em}p\textit{é}rim\textit{è}tre \ du \ triangle \\
p = \frac{a+b+c}{2}
\end{gather*} $$
Démonstrations
Formule de l'aire
Pour le démontrer, projectons une hauteur \( h_c \) sur la longueur \( c \), et telle que la figure suivante :
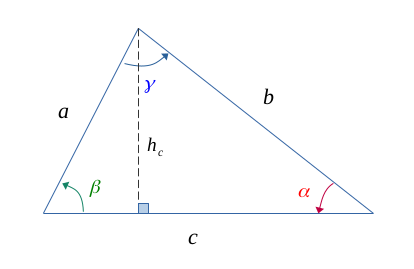
Immédiatement, il vient les relations suivantes :
Par suite, il vient que :
Or, la formule de l'aire du triangle \(\{a, b, c\}\) est :
$$ S_{abc} = \frac{1}{2}c.h_c \qquad (\mathcal{A}) $$
Maintenant, en injectant les valeurs de \(h_c\) provenant de \((1')\) et \((2')\) dans celle de \((\mathcal{A})\), on a la double égalité :
Enfin, en projetant une des deux autres hauteurs, on retrouve la troisième égalité, et finalement :
$$\forall (a, b, c) \in \hspace{0.05em} \mathbb{R}^3,$$
Formule de Héron
Pour démontrer cette formule, on projette comme précédemment la hauteur \( h_c \) sur la longueur \( c \) :

Grâce au théorème d'Al-Kashi, on a la relation suivante :
$$ a^2 + b^2 - 2ab.cos(\gamma) = c^2 $$
$$ a^2 + b^2 - c^2 = 2ab.cos(\gamma) $$
Et par suite,
$$ \frac{a^2 + b^2 - c^2}{2ab} = cos(\gamma) \qquad (3) $$
Or, on sait que :
$$ sin^2(\gamma) = 1 - cos^2(\gamma) $$
$$ sin^2(\gamma) = \bigl(1 - cos(\gamma)\bigr)\bigl(1 + cos(\gamma)\bigr) \qquad (4) $$
En injectant maintenant l'expression \((3)\) dans l'expression \((4)\), on a :
$$ sin^2(\gamma) = \left(1 - \frac{a^2 + b^2 - c^2}{2ab} \right)\left(1 + \frac{a^2 + b^2 - c^2}{2ab}\right) $$
$$ sin^2(\gamma) = \left(\frac{2ab}{2ab} - \frac{a^2 + b^2 - c^2}{2ab} \right)\left(\frac{2ab}{2ab} + \frac{a^2 + b^2 - c^2}{2ab}\right) $$
$$ sin^2(\gamma) = \left(\frac{2ab - (a^2 + b^2 - c^2)}{2ab} \right)\left(\frac{2ab + (a^2 + b^2 - c^2) }{2ab}\right) $$
$$ sin^2(\gamma) = \left(\frac{2ab - a^2 - b^2 + c^2}{2ab} \right)\left(\frac{2ab + a^2 + b^2 - c^2 }{2ab}\right) $$
On s'arrange pour retrouver les deux premières identités remarquables :
$$ sin^2(\gamma) = \left(\frac{-(a^2 + b^2 - 2ab) + c^2}{2ab} \right)\left(\frac{a^2 + b^2 + 2ab - c^2 }{2ab}\right) $$
$$ sin^2(\gamma) = \left(\frac{c^2 -(a-b)^2}{2ab} \right)\left(\frac{(a+b)^2 - c^2 }{2ab}\right) $$
Et on factorise maintenant à l'aide de la troisième identité remarquable :
$$ sin^2(\gamma) = \left(\frac{\bigl(c - (a-b)\bigr)\bigl(c + (a-b)\bigr)}{2ab} \right)\left(\frac{ \bigl((a+b) -c \bigr)\bigl((a+b) + c \bigr)}{2ab}\right) $$
On retire les parenthèses :
$$ sin^2(\gamma) = \left(\frac{(c-a+b)(c+a-b) }{2ab} \right)\left(\frac{ (a+b-c)(a+b+c) }{2ab}\right)$$
$$ sin^2(\gamma) = \frac{(c-a+b)(c+a-b)(a+b-c)(a+b+c)}{4a^2b^2} \qquad (5) $$
Par ailleurs, on a vu plus avec la formule de l'aire que :
$$ S_{abc} = \frac{1}{2}ab . sin(\gamma) $$
Et alors aussi que :
$$ (S_{abc})^2 = \frac{1}{4}a^2b^2 . sin^2(\gamma) \qquad (6)$$
Alors, en injectant l'expression \((5)\) dans l'expression \((6)\), on a :
$$ (S_{abc})^2 = \frac{1}{4}a^2b^2 . \frac{(c-a+b)(c+a-b)(a+b-c)(a+b+c)}{4a^2b^2}$$
En remettant les éléments en ordre, on a :
$$ (S_{abc})^2 = \frac{1}{16}(a+b+c) (a+b-c)(b+c-a)(a+c-b) $$
À ce stade, introduisons le périmétre \(P\) du triangle, alors l'expression devient :
$$ (S_{abc})^2 = \frac{1}{16}P (P - 2c)(P - 2a)(P - 2b) $$
Puis celle de demi-périmètre \(p\) :
$$ (S_{abc})^2 = \frac{1}{16}2p (2p - 2c)(2p - 2a)(2p - 2b) $$
On factorise toutes les expressions entre parenthèses par \(2\) :
$$ (S_{abc})^2 = \frac{1}{16} \times 2p \times 2(p - c) \times 2(p - a) \times 2(p - b) $$
$$ (S_{abc})^2 = p (p - c)(p - a)(p - b) $$
Soit finalement,
$$\forall (a, b, c) \in \hspace{0.05em} \mathbb{R}^3,$$
$$ S_{abc} = \sqrt{p(p-a)(p-b)(p-c)} \qquad (Héron) $$
$$ avec \enspace \Biggl \{ \begin{gather*}
p : demi\hspace{-0.3em}-\hspace{-0.3em}p\textit{é}rim\textit{è}tre \ du \ triangle \\
p = \frac{a+b+c}{2}
\end{gather*} $$











 Retour en haut de page
Retour en haut de page