The right-angled triangle inscribed in a circle

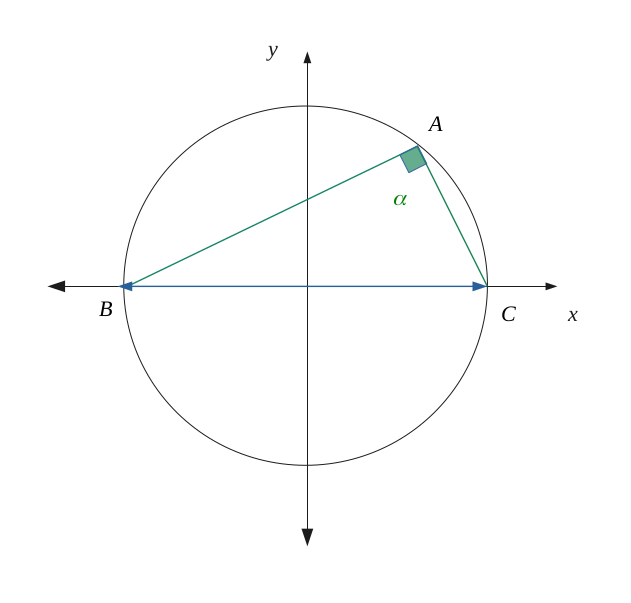
In a circle, if an inscribed triangle has the diameter of this circle as its longest side, then this triangle will be right-angled.

Demonstration

To do this, let us consider an orthonomous coordinate system $ (0, \vec{x}, \vec{y}) $.

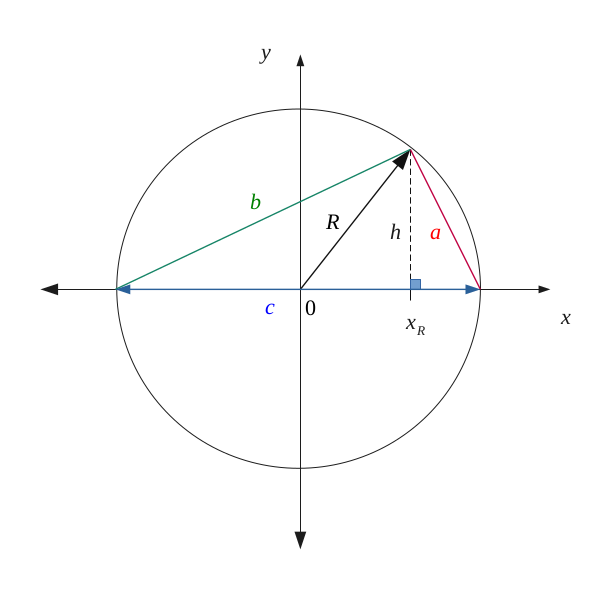
We called the sides of the triangle $ a, b, c $, and we projected a height $ h $ along the length $ c $, with as a point of intersection $ x_R $ .

Likewise, we traced the radius $ R $ of the circle pointing towards the vertex between $ a $ and $ b $ of the triangle.

We will seek to demonstrate that the triangle $ \{a, b, c \} $ is right-angled between both sides $ a $ and $ b $.

$$ a^2 + b^2 = c^2 \Longrightarrow a \perp b \qquad \bigl(Pythagore \enspace(reciprocal) \bigr) $$

C'est ce que nous allons démontrer.

We apply the Pythagorean Theorem on three right-angled triangles:

- that formed by $ \{h, (R - x_r), a \} $

- that formed by $ \{h, (R + x_r), b\} $

- that formed by $ \{h, x_R, R \} $

We then have the following equalities:

$$ h^2 + (R - x_R)^2 = a^2 \qquad (1) $$

$$ h^2 + (R + x_R)^2 = b^2 \qquad (2) $$

$$ h^2 + x_R^2 = R^2 \Longleftrightarrow h^2 = R^2 - x_R^2\qquad (3) $$

Let us inject the expression of $ h^2 $ of the expression $ (3) $ into $ (1) $ and $ (2) $, we then obtain a new pair of equality:

$$ \Biggl \{ \begin{gather*} R^2 - x_R^2 + (R - x_R)^2 = a^2 \qquad (4) \\ R^2 - x_R^2 + (R + x_R)^2 = b^2 \qquad (5) \end{gather*} $$

Let us now calculate $ a^2 + b^2 $ by performing $ (4) + (5) $:

$$ a^2 + b^2 = R^2 - x_R^2 + (R - x_R)^2 + R^2 - x_R^2 + (R + x_R)^2 $$

$$ a^2 + b^2 = R^2 - x_R^2 + R^2 - 2R.x_R + x_R^2 + R^2 - x_R^2 + R^2 + 2R.x_R + x_R^2 $$

Many terms cancel, and we obtain:

$$ a^2 + b^2 = 4R^2 $$

$$ a^2 + b^2 = (2R)^2 $$

Moreover, we know that:

$$ c = 2R $$

Because it is our diameter by hypothesis.

And finally,

$$ a^2 + b^2 = c^2 $$

With the Pythagorean Theorem reciprocal, we showed that the triangle $ \{a, b, c \} $ is right-angled between the sides $ a $ and $ b $.

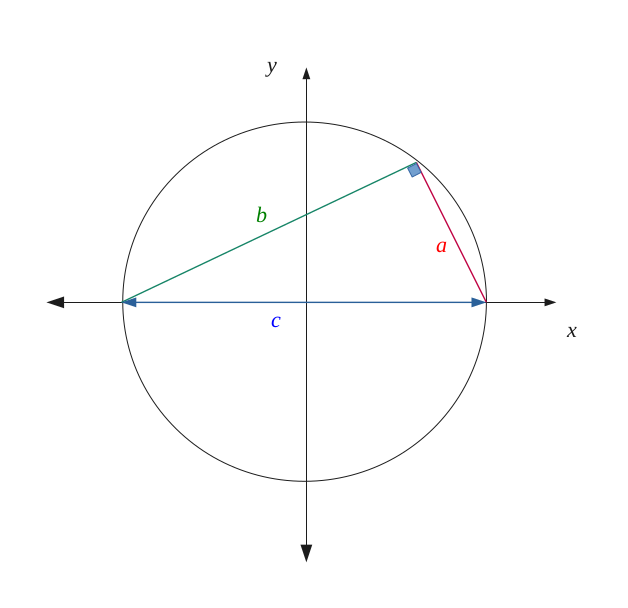
Thus,

In a circle, if an inscribed triangle has the diameter of this circle as its longest side, then this triangle will be right-angled.

Go to the top of the page