The properties of the vector product

Let \( \vec{u}\) and \( \vec{v}\) be two non-null vectors.

We call vector product (or cross product of two vectors) \( \vec{u} \land \vec{v} \), a new vector extracted from \( \vec{u}\) and \( \vec{v}\) such as:

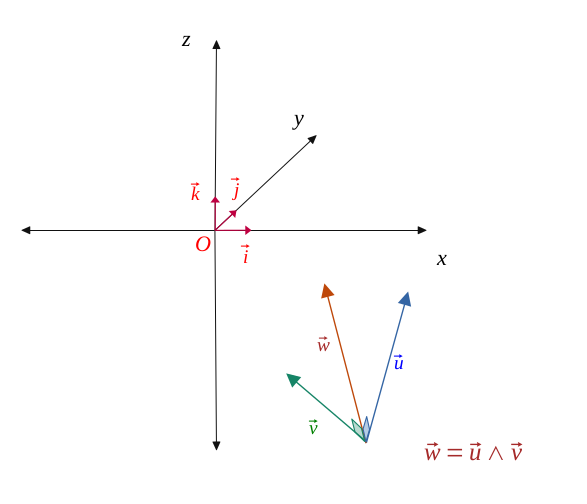
The vector product \( \vec{u} \land \vec{v} \) is orthogonal to both vectors \( \vec{u}\) and \( \vec{v}\).

Cartesian coordinates

Norm

Lagrange's identity

Collinearity of two vectors

Anticommutative law

Distributive law in relation to the addition

And also the distributive law to the left:

Freedom of the constant

Gibbs' formula

Jacobi's identity

Recap table of the properties of the vector product

Click on the title to access to the recap table.

---

Demonstrations

Cartesian coordinates

Let \(\vec{u}\begin{pmatrix} x_1\\ y_1\\z_1 \end{pmatrix}\) and \(\vec{v}\begin{pmatrix} x_2\\ y_2\\z_2 \end{pmatrix}\) be two non-null vectors.

We are looking for a vector \( \vec{w} \begin{pmatrix} x\\ y\\z \end{pmatrix} \) orthogonal to these two vectors, and such as the following figure:

The two vectors \( \vec{u}\) and \( \vec{v}\) being respectively orthogonal to the vector \( \vec{w}\), we do have:

$$ \Biggl \{ \begin{gather*} \vec{u}.\vec{w} = 0 \\ \vec{v}.\vec{w} = 0\end{gather*} $$

So,

$$ \Biggl \{ \begin{gather*} x. x_1 + y. y_1 + z. z_1 = 0 \\ x. x_2 + y. y_2 + z. z_2 = 0\end{gather*} $$

$$ \Biggl \{ \begin{gather*} x. x_1 + y. y_1 = - z. z_1 \\ x. x_2 + y. y_2 = - z. z_2 \end{gather*} $$

And then,

$$ (S) \enspace \left \{ \begin{gather*} \frac{x}{z}. x_1 + \frac{y}{z}. y_1 = - z_1 \\ \\ \frac{x}{z} . x_2 + \frac{y}{z}. y_2 = - z_2 \end{gather*} \right \} $$

Let us solve the system \((S)\).

We divide both equations respectively by \(x_1\) and \(x_2\), in order to isolate \(\frac{x}{z}\).

$$ (S) \Longleftrightarrow \left \{ \begin{gather*} \frac{x}{z} + \frac{y}{z}. \frac{y_1}{x_1} = - \frac{z_1}{x_1} \\ \\ \frac{x}{z} + \frac{y}{z}. \frac{y_2}{x_2} = - \frac{z_2}{x_2} \end{gather*} \right \} $$

$$ (S) \Longleftrightarrow \left \{ \begin{gather*} \frac{x}{z} = - \frac{y}{z}. \frac{y_1}{x_1} - \frac{z_1}{x_1} \\ \\ \frac{x}{z} = - \frac{y}{z}. \frac{y_2}{x_2} - \frac{z_2}{x_2} \end{gather*} \right \} $$

We then have a similar value for \(\frac{x}{z}\), hence the equality:

Finally, by putting the two members under the same denominator, we do obtain:

Let us do the same thing for \(\frac{x}{z}\).

Starting from the initial form of \((S)\), we now divide the two equations respectively by \(y_1\) and \(y_2\).

$$ (S) \enspace \left \{ \begin{gather*} \frac{x}{z}. x_1 + \frac{y}{z}. y_1 = - z_1 \\ \\ \frac{x}{z} . x_2 + \frac{y}{z}. y_2 = - z_2 \end{gather*} \right \} $$

$$ (S) \Longleftrightarrow \left \{ \begin{gather*} \frac{x}{z}.\frac{x_1}{y_1} + \frac{y}{z} = - \frac{z_1}{y_1} \\ \\ \frac{x}{z}.\frac{x_2}{y_2} + \frac{y}{z} = - \frac{z_2}{y_2} \end{gather*} \right \} $$

$$ (S) \Longleftrightarrow \left \{ \begin{gather*} \frac{y}{z} = - \frac{x}{z}.\frac{x_1}{y_1} - \frac{z_1}{y_1} \\ \\ \frac{y}{z} = - \frac{x}{z}.\frac{x_2}{y_2} - \frac{z_2}{y_2} \end{gather*} \right \} $$

Hence the equality:

Now, thanks to both equalities \((1)\) and \((2)\), we extract two new from it:

These two equalities \((1')\) and \((2')\) having a common term, so all these three ratios are equal:

The coordinates \((x, y, z)\) being themselves defined up to a constant, by applying this ratio for \( k = 1 \), we do obtain the coordinates of \( \vec{w} \):

And as a result,

Norm

Let \(\vec{u}\begin{pmatrix} x_1\\ y_1\\z_1 \end{pmatrix}\) and \(\vec{v}\begin{pmatrix} x_2\\ y_2\\z_2 \end{pmatrix}\) be two non-null vectors.

So, using the cartesian coordinates seen above, we do have:

So, by developing it:

$$ || \vec{u} \land \vec{v} || = \sqrt{ \begin{gather*} \Bigl(y_1^2.z_2^2 - 2 y_1.z_2.y_2.z_1 + y_2^2.z_1^2 \Bigr) + \Bigl(x_2^2.z_1^2 - 2 x_2.z_1.x_1.z_2 + x_1^2.z_2^2 \Bigr) + \Bigl(x_1^2.y_2^2 - 2 x_1.y_2.x_2.y_1 + x_2^2.y_1^2 \Bigr) \end{gather*} } $$

$$ || \vec{u} \land \vec{v} || = \sqrt{ \Bigl(x_1.y_2 \Bigr)^2 + \Bigl(x_1.z_2 \Bigr)^2 + \Bigl(y_1.x_2 \Bigr)^2 + \Bigl(y_1.z_2 \Bigr)^2 + \Bigl(z_1.x_2 \Bigr)^2 + \Bigl(z_1.y_2 \Bigr)^2 - 2 y_1.z_2.y_2.z_1 - 2 x_2.z_1.x_1.z_2 - 2 x_1.y_2.x_2.y_1 } $$

We notice that the left part of the square root almost corresponds to the product \( \Bigl(x_1^2 + y_1^2 + z_1^2 \Bigr) \Bigl(x_2^2 + y_2^2 + z_2^2 \Bigr)\). Effectively:

$$ \Bigl(x_1.y_2 \Bigr)^2 + \Bigl(x_1.z_2 \Bigr)^2 + \Bigl(y_1.x_2 \Bigr)^2 + \Bigl(y_1.z_2 \Bigr)^2 + \Bigl(z_1.x_2 \Bigr)^2 + \Bigl(z_1.y_2 \Bigr)^2 = \Bigl(x_1^2 + y_1^2 + z_1^2 \Bigr) \Bigl(x_2^2 + y_2^2 + z_2^2 \Bigr) - \Bigl(x_1.x_2 \Bigr)^2 - \Bigl(y_1.y_2 \Bigr)^2 - \Bigl(z_1.z_2 \Bigr)^2 $$

We then have:

$$ || \vec{u} \land \vec{v} || = \sqrt{ \Bigl(x_1^2 + y_1^2 + z_1^2 \Bigr) \Bigl(x_2^2 + y_2^2 + z_2^2 \Bigr) - \Bigl(x_1.x_2 \Bigr)^2 - \Bigl(y_1.y_2 \Bigr)^2 - \Bigl(z_1.z_2 \Bigr)^2 - 2 y_1.z_2.y_2.z_1 - 2 x_2.z_1.x_1.z_2 - 2 x_1.y_2.x_2.y_1 } $$

$$ || \vec{u} \land \vec{v} || = \sqrt{ \Bigl(x_1^2 + y_1^2 + z_1^2 \Bigr) \Bigl(x_2^2 + y_2^2 + z_2^2 \Bigr) - \biggl[ \Bigl(x_1.x_2 \Bigr)^2 + \Bigl(y_1.y_2 \Bigr)^2 + \Bigl(z_1.z_2 \Bigr)^2 + 2 \left(x_1.x_2 \right) \left(y_1.y_2 \right) + 2 \left(y_1.y_2 \right) \left(z_1.z_2 \right) + 2 \left(x_1.x_2 \right)\left(z_1.z_2 \right) \biggr] } $$

Likewise, by restoring a little order, we see another remarkable identity:

So in our case:

$$ || \vec{u} \land \vec{v} || = \sqrt{ \Bigl(x_1^2 + y_1^2 + z_1^2 \Bigr) \Bigl(x_2^2 + y_2^2 + z_2^2 \Bigr) - \biggl[ x_1.x_2 + y_1.y_2 + z_1.z_2 \biggr]^2 } $$

We recognize certain formulas of the scalar product.

$$ || \vec{u} \land \vec{v} || = \sqrt{ {|| \vec{u} ||}^2 \times {|| \vec{v} ||}^2 - \bigl( \vec{u}.\vec{v} \bigr)^2 } \qquad (3) $$

$$ || \vec{u} \land \vec{v} || = \sqrt{ {|| \vec{u} ||}^2 \times {|| \vec{v} ||}^2 - \biggl[ || \vec{u}|| \times || \vec{v}|| \times cos(\vec{u}, \vec{v})\biggr]^2 } $$

$$ || \vec{u} \land \vec{v} || = \sqrt{ \biggl( || \vec{u}|| \times || \vec{v}|| \biggr)^2 \biggl( 1 - cos^2(\vec{u}, \vec{v})\biggr) } $$

And as a result,

Lagrange's identity

In the previous section, we found out the equation \((3)\):

$$ || \vec{u} \land \vec{v} || = \sqrt{ {|| \vec{u} ||}^2 \times {|| \vec{v} ||}^2 - \bigl( \vec{u}.\vec{v} \bigr)^2 } \qquad (3) $$

By applying the square on both sides of this equation, we do obtain the Lagrange's identity:

Collinearity of two vectors

Let \(\vec{u}\begin{pmatrix} x_1\\ y_1\\z_1 \end{pmatrix}\) and \(\vec{v}\begin{pmatrix} x_2\\ y_2\\z_2 \end{pmatrix}\) be two non-null vectors.

1. From left to right implication

Let us start from the hypothesis that \(\vec{u} \) and \(\vec{v} \) are collinear.

So, we have the relationship:

$$ \exists k \in \mathbb{R}, \ \vec{u} = k. \vec{v} $$

And the vector \(\vec{u}\) can be written in terms of \(\vec{v}\):

$$ \vec{u}\begin{pmatrix} x_1\\ y_1\\z_1 \end{pmatrix} = k .\vec{v}\begin{pmatrix} x_2\\ y_2\\z_2 \end{pmatrix} = \vec{u}\begin{pmatrix} k . x_2 \\ k . y_2 \\ k . z_2 \end{pmatrix}$$



By determining the coordinates of \( \vec{u} \land \vec{v} \), we do have:

$$ \vec{u} \land \vec{v} = \begin{pmatrix} k . x_2 \\ k . y_2 \\ k . z_2 \end{pmatrix} \land \begin{pmatrix} x_2\\ y_2\\z_2 \end{pmatrix} = \begin{pmatrix} k.y_2.z_2 - y_2.k.z_2 \\ x_2.k.z_2 - k.x_2.z_2 \\ k.x_2.y_2 - x_2.k.y_2 \end{pmatrix} $$
$$ \vec{u} \land \vec{v} = \vec{0} $$



2. Reciprocal

Let us now start from the hypothesis that \(\vec{u} \land \vec{v} = \vec{0}\).

So, its norm is worth zero.

$$ || \vec{u} \land \vec{v} || = || \vec{u}|| \times || \vec{v}|| \times sin(\vec{u}, \vec{v}) = 0$$

And as by hypothesis our two vectors are not zero, then we necessarily have:

$$ || \vec{u} \land \vec{v} || = 0 \ \Longrightarrow \ sin(\vec{u}, \vec{v}) = 0$$

And,

$$ \forall k \in \mathbb{N}, \ sin(\vec{u}, \vec{v}) = 0 \ \Longrightarrow \ \Biggl\{ (\vec{u}, \vec{v}) = k\pi \Biggr\} $$

Then the two vectors are collinear.




3. Conclusion

$$ \forall (\vec{u}, \vec{v}) \neq \vec{0},$$
$$ \vec{u} \ and \ \vec{v} \ collinear \Longleftrightarrow \vec{u} \land \vec{v} = \vec{0} $$

In a general way, it makes no sense to look for a unique vector orthogonal to two collinear vectors, because there exist an infinite of it.

Anticommutative law

Let \(\vec{u}\begin{pmatrix} x_1\\ y_1\\z_1 \end{pmatrix}\) and \(\vec{v}\begin{pmatrix} x_2\\ y_2\\z_2 \end{pmatrix}\) be two non-null vectors.

Let us calculate the coordinates of \( \vec{u} \land \vec{v} \) and \( \vec{v} \land \vec{u} \).

And as a result,

Distributive law in relation to the addition

Let \(\vec{u}\begin{pmatrix} x_1\\ y_1\\z_1 \end{pmatrix}\), \(\vec{v}\begin{pmatrix} x_2\\ y_2\\z_2 \end{pmatrix}\) and \(\vec{w}\begin{pmatrix} x_3\\ y_3\\z_3 \end{pmatrix}\) be three non-null vectors.

1. Distributive law to the right

Let us calculate the coordinates of \( \vec{u} \land ( \vec{v} + \vec{w}) \).

$$\vec{u} \land ( \vec{v} + \vec{w}) = \begin{pmatrix} x_1\\ y_1\\z_1 \end{pmatrix} \land \begin{pmatrix} x_2 + x_3\\ y_2 + y_3 \\ z_2 + z_3 \end{pmatrix} $$
$$\vec{u} \land ( \vec{v} + \vec{w}) = \begin{pmatrix} y_1.\bigl[z_2 + z_3\bigr] - \bigl[y_2 + y_3 \bigr].z_1 \\ \bigl[x_2 + x_3\bigr].z_1 - x_1.\bigl[ z_2 + z_3 \bigr] \\ x_1.\bigl[y_2 + y_3 \bigr] -\bigl[x_2 + x_3 \bigr].y_1 \end{pmatrix} $$
$$\vec{u} \land ( \vec{v} + \vec{w}) = \begin{pmatrix} y_1.z_2 + y_1.z_3 - y_2.z_1 - y_3.z_1 \\ x_2.z_1 + x_3.z_1 - x_1.z_2 - x_1.z_3 \\ x_1.y_2 + x_1.y_3 - x_2.y_1 - x_3.y_1\end{pmatrix} $$

But, the vector products \( \vec{u} \land \vec{v} \) and \( \vec{u} \land \vec{w} \) are respectively worth:

$$ \vec{u} \land \vec{v} = \begin{pmatrix} y_1.z_2 - y_2.z_1 \\ x_2.z_1 - x_1.z_2 \\ x_1.y_2 - x_2.y_1 \end{pmatrix} $$
$$ \vec{u} \land \vec{w} = \begin{pmatrix} y_1.z_3 - y_3.z_1 \\ x_3.z_1 - x_1.z_3 \\ x_1.y_3 - x_3.y_1 \end{pmatrix} $$



And as a result,

$$ \forall (\vec{u}, \vec{v}, \vec{w}) \neq \vec{0},$$
$$ \vec{u} \land ( \vec{v} + \vec{w}) = \vec{u} \land \vec{v} + \vec{u} \land \vec{w} $$


2. Distributive law to the left

Thanks to the anticommutative law, we do have:

$$ (\vec{u} + \vec{v}) \land \vec{w}= - \ w \land ( \vec{u} + \vec{v}) $$

Now, distributing it to the right:

$$ (\vec{u} + \vec{v}) \land \vec{w}= - \vec{w} \land \vec{u} - \vec{w} \land \vec{v} $$

In the end, applying again the anticommutative law:

$$ (\vec{u} + \vec{v}) \land \vec{w}= \vec{u} \land \vec{w} + \vec{v} \land \vec{w} $$



And as a result,

$$ \forall (\vec{u}, \vec{v}, \vec{w}) \neq \vec{0},$$
$$(\vec{u} + \vec{v}) \land \vec{w}= \vec{u} \land \vec{w} + \vec{v} \land \vec{w} $$

Freedom of the constant

Let \(\vec{u}\begin{pmatrix} x_1\\ y_1\\z_1 \end{pmatrix}\) and \(\vec{v}\begin{pmatrix} x_2\\ y_2\\z_2 \end{pmatrix}\) be two non-null vectors.

When we perform \( \lambda (\vec{u} \land \vec{v} ) \), we notice that:

But,

And in the same way on the right,

All three expressions are equal.

And as a result,

Gibbs' formula

Let \(\vec{u}\begin{pmatrix} x_1\\ y_1\\z_1 \end{pmatrix}\), \(\vec{v}\begin{pmatrix} x_2\\ y_2\\z_2 \end{pmatrix}\) and \(\vec{w}\begin{pmatrix} x_3\\ y_3\\z_3 \end{pmatrix}\) be three non-null vectors.

Let us calculate a vector product of vector product: \( \vec{u} \land (\vec{v} \land \vec{w})\).

By factorizing, we notice that up to a term appear some scalar product:

And as a result,

Jacobi's identity

Let \(\vec{u}\begin{pmatrix} x_1\\ y_1\\z_1 \end{pmatrix}\), \(\vec{v}\begin{pmatrix} x_2\\ y_2\\z_2 \end{pmatrix}\) and \(\vec{w}\begin{pmatrix} x_3\\ y_3\\z_3 \end{pmatrix}\) be three non-null vectors.

If we want to calculate three vector products of vector product, shifting each vector to the right, we do have:

Thanks to the Gibbs' formula previously calculated, we will be able to easily simplify this expression.

And as a result,

Recap table of the properties of the vector product

---

Examples

1. Determining the equation of a plane in space

Let \((ABCDEFGH)\) be a cube in an orthonormal coordinate system in space \((A, \ \overrightarrow{AB}, \ \overrightarrow{AD}, \ \overrightarrow{AE})\).



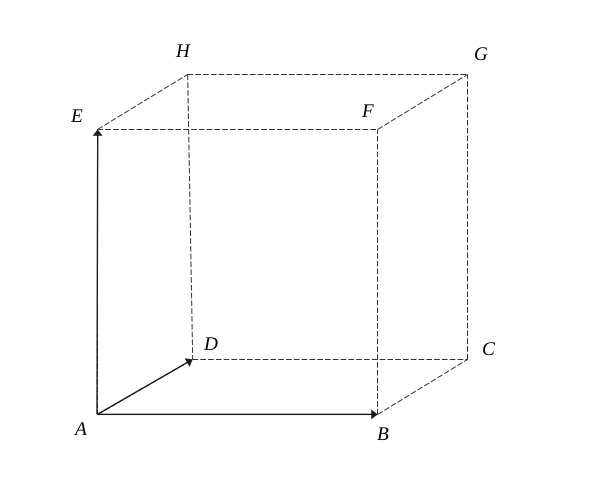
We want to determine the equation of the plane \((BGE)\).

To do this, we need to first determine the vector \( \vec{n}\) orthogonal to this plane, by performing the vector product of to vectors of this plane.



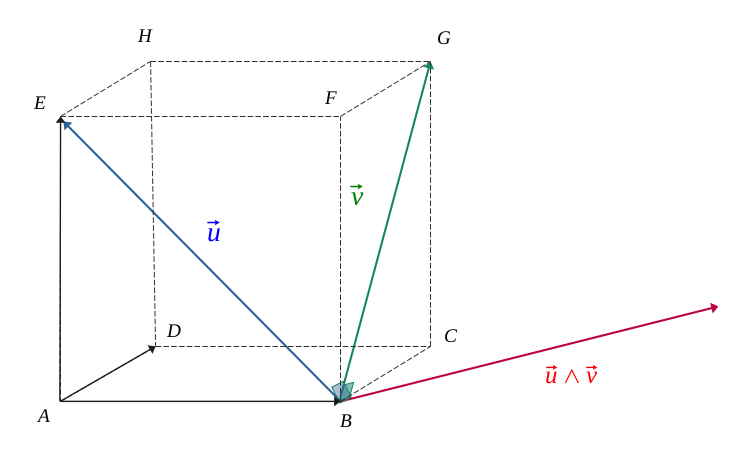
By making the arbitrary choice of the two vectors \(\vec{u} = \ \overrightarrow{BE}\) et \(\vec{v} = \ \overrightarrow{BG}\),we do have:

$$ \vec{u} \land \vec{v} = \ \overrightarrow{BE} \land \ \overrightarrow{BG} $$
$$ \vec{u} \land \vec{v} = \ \begin{pmatrix} x_E - x_ B \\ y_E - y_ B \\ z_E - z_ B\end{pmatrix} \land \begin{pmatrix} x_G - x_ B \\ y_G - y_ B \\ z_G - z_ B\end{pmatrix} $$
$$ \vec{u} \land \vec{v} = \begin{pmatrix} -1 \\ \ \ \ 0 \\ \ \ \ 1 \end{pmatrix} \land \begin{pmatrix} 0 \\ 1\\ 1\end{pmatrix} $$
$$ \vec{u} \land \vec{v} = \begin{pmatrix} 0 \times 1 - 1 \times 1 \\ 0 \times 1 - (-1) \times 1 \\ (-1) \times 1 - 0 \times 0 \end{pmatrix} $$
$$ \vec{u} \land \vec{v} = \begin{pmatrix} -1 \\ \ \ \ 1 \\ -1 \end{pmatrix} $$

The plane \((BGE)\) has for normal vector \( \vec{n} \begin{pmatrix} -1 \\ \ \ \ 1\\ -1 \end{pmatrix} \), and then have as equation:

$$ -x + y -z + d = 0 \qquad (BGE) $$



Let us finally determine the parameter \(d\) by injecting the coordinates of a point of this plane in its equation; point \(B\) for example.

$$ x_B + y_B -z_B + d = 0 $$
$$ -1 + 0 -0 + d = 0 \ \Longrightarrow \ d = 1$$

And as a result the equation of the plane \((BGE)\) is worth:

$$ -x + y -z +1 = 0 \qquad (BGE) $$