The properties of the scalar product
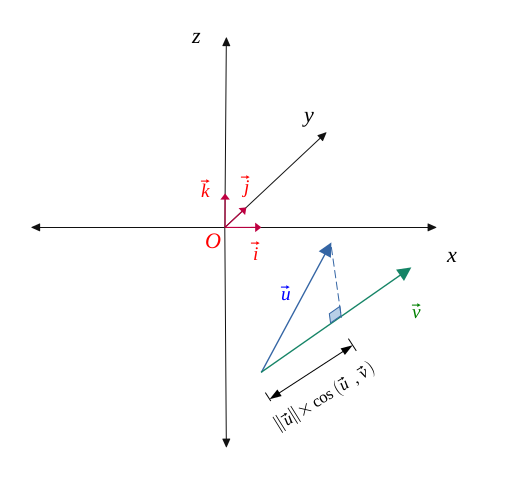
Let \( \vec{u}\) and \( \vec{v}\) be two vectors.
We represent \(||\vec{u}|| \) and \(||\vec{v}|| \) as the respective magnitudes of \( \vec{u}\) and \( \vec{v}\), and \( (\vec{u} , \vec{v})\) the forming angle by these two vectors.
We call the scalar product \( \vec{u}.\vec{v} \), the real number resulting from:
$$ \vec{u}.\vec{v} = ||\vec{u}|| \times ||\vec{v}|| \times cos(\vec{u}, \vec{v}) $$
This is the magnitude of the orthogonal projection of the vector \( \vec{u}\) onto the vector \( \vec{v}\), multiplied by the magnitude of the vector \( \vec{v}\).
$$ \forall (\vec{u}, \vec{v}), $$
$$ \vec{u} . \vec{v} = \vec{v}. \vec{u} $$
$$ \forall (\vec{u}, \vec{v}) \neq \vec{0},$$
$$ \vec{u} \text{ and } \vec{v} \text{ orthogonal vectors } \Longleftrightarrow \vec{u}. \vec{v} = 0 $$
$$ \forall \vec{u},$$
$$ \vec{u}.\vec{u} = {|| \vec{u} ||}^2 $$
$$ \forall \left [\vec{u}\begin{pmatrix} x\\ y\\z \end{pmatrix} , \vec{v}\begin{pmatrix} x'\\ y'\\z' \end{pmatrix} \right], $$
$$ \vec{u}. \vec{v} = xx' + yy' +zz' $$
$$ \forall \lambda \in \hspace{0.04em} \mathbb{R}, \ \forall (\vec{u}, \vec{v}),$$
$$ (\lambda\vec{u}).\vec{v} = \vec{u}.(\lambda\vec{v}) = |\lambda| \times \vec{u}. \vec{v}$$
Furthermore, performing the scalar product \( (\lambda\vec{u}).(\mu\vec{v})\), we do obtain:
$$ \forall (\lambda, \mu) \in \hspace{0.04em} \mathbb{R}^2, \ \forall (\vec{u}, \vec{v}),$$
$$ (\lambda\vec{u}).(\mu\vec{v}) = |\lambda| \times |\mu| \times \vec{u}. \vec{v} $$
$$ \forall (\vec{u}, \vec{v}, \vec{w}), $$
$$ \vec{u}.( \vec{v} + \vec{w}) = \vec{u}.\vec{v} + \vec{u}.\vec{w} $$
And also the distributive law to the left:
$$ \forall (\vec{u}, \vec{v}, \vec{w}), $$
$$ (\vec{u} + \vec{v}) . \vec{w} = \vec{u}.\vec{w} + \vec{v}.\vec{w} $$
These are the same formulas as remarkable identities.
$$ \forall (\vec{u}, \vec{v}), $$
$$ (\vec{u} + \vec{v})^2 = {|| \vec{u} ||}^2 + 2 \vec{u}.\vec{v} + {|| \vec{v} ||}^2 $$
$$ (\vec{u} - \vec{v})^2 = {|| \vec{u} ||}^2 - 2 \vec{u}.\vec{v} + {|| \vec{v} ||}^2 $$
$$ {|| \vec{u} ||}^2 - {|| \vec{v} ||}^2= (\vec{u} + \vec{v}) (\vec{u} - \vec{v}) $$
$$ \forall (\vec{u}, \vec{v}), $$
$$ \vec{u}.\vec{v} =\frac{1}{2} \left( {|| \vec{u} + \vec{v} ||}^2 - {|| \vec{u} ||}^2 - {|| \vec{v} ||}^2 \right ) $$
$$ \vec{u}.\vec{v} =\frac{1}{2} \left( {|| \vec{u} ||}^2 + {|| \vec{v} ||}^2 - {|| \vec{u} -\vec{v} ||}^2 \right ) $$
$$ \forall (\vec{u}, \vec{v}), $$
The vectorial projection of \(\vec{u}\) onto \(\vec{v}\) is worth:
$$ \overrightarrow{proj}_{\mathcal{(\vec{u})}} \hspace{0.1em} \bigl(\vec{v}\bigr) = \frac{(\vec{u}.\vec{v})}{||\vec{u}||^2}. \vec{u} $$

Click on the title to access to the recap table.
Demonstrations
Let \(\vec{u} \) and \(\vec{v} \) be two vectors.
Performing both scalar products \( \vec{u}.\vec{v} \) and \( \vec{v}.\vec{u} \), we do have:
$$ \Biggl \{ \begin{gather*}
\vec{u}.\vec{v} = ||\vec{u}|| \times ||\vec{v}|| \times cos(\vec{u}, \vec{v}) \\
\vec{v}.\vec{u} = ||\vec{v}|| \times ||\vec{u}|| \times cos(\vec{v}, \vec{u}) \end{gather*} $$
Let us call \(\alpha \) = \( (\vec{u}, \vec{v}) \), the forming angle by \( \vec{u} \) and \(\vec{v} \), then:
$$ \Biggl \{ \begin{gather*}
cos(\alpha ) = cos(\vec{u}, \vec{v}) \\
cos( - \alpha ) = cos(\vec{v}, \vec{u}) \end{gather*} $$
But, the cosine function is pair and: \( \forall \alpha \in \mathbb{R}, \ cos(\alpha ) = cos(-\alpha ) \).
From this we can deduce that: \( cos(\vec{u}, \vec{v}) = cos(\vec{v}, \vec{u}) \).
And finally,
$$ \forall (\vec{u}, \vec{v}), $$
$$ \vec{u}.\vec{v} =\vec{v}.\vec{u} $$
Let \(\vec{u} \) and \(\vec{v} \) be two vectors, different from the zero vector.
-
From left to right implication
Let us assume that \(\vec{u} \) and \(\vec{v} \) are orthogonal.
Then, by the definition of the scalar product,
$$ \vec{u}.\vec{v} = ||\vec{u}|| \times ||\vec{v}|| \times cos(\vec{u}, \vec{v}) $$
But, if \(\vec{u} \) ans \(\vec{v} \) are orhtogonal, then \(cos(\vec{u}, \vec{v}) = cos \left(\frac{\pi}{2}\right) = 0 \).
Thus, their scalar product will be zero, and:
$$ \forall (\vec{u}, \vec{v}) \neq \vec{0},$$
$$ \vec{u} \text{ et } \vec{v} \text{ orthogonal vectors }\Longrightarrow \vec{u}. \vec{v} = 0 $$
-
Reciprocal
Reciprocally, being said that the two vectors \(\vec{u} \) and \(\vec{v} \) are non-zero vectors, so:
$$ \vec{u}. \vec{v} = 0 \Longrightarrow cos(\vec{u}, \vec{v}) = 0 $$
And,
$$ \forall k \in \mathbb{N}, \ cos(\vec{u}, \vec{v}) = 0 \Longrightarrow \Biggl\{ (\vec{u}, \vec{v}) = \frac{k\pi}{2} \Biggr \} $$
And as a result, \(\vec{u} \) and \(\vec{v} \) are necessarily orthogonal vectors.
$$\vec{u}. \vec{v} = 0 \Longrightarrow \vec{u} \text{ et } \vec{v} \text{ orthogonal vectors }$$
-
Conclusion
$$ \forall (\vec{u}, \vec{v}) \neq \vec{0},$$
$$ \vec{u} \text{ et } \vec{v} \text{ orthogonal vectors }\Longleftrightarrow \vec{u}. \vec{v} = 0 $$
Let \(\vec{u} \) be a vector.
Then, by the definition of the scalar product,
$$ \vec{u}.\vec{u} = ||\vec{u}|| \times ||\vec{u}|| \times cos(\vec{u}, \vec{u}) $$
But \(cos(\vec{u}, \vec{u}) = cos \left(0\right) = 1 \).
Thus, only magnitudes remains in the product.
And finally:
$$ \forall \vec{u},$$
$$ \vec{u}.\vec{u} = {|| \vec{u} ||}^2 $$
Let \(\vec{u}\begin{pmatrix} x\\ y\\z \end{pmatrix}\) and \(\vec{v}\begin{pmatrix} x'\\ y'\\z' \end{pmatrix}\) be two vectors represented in an orthonormal coordinate system \( (O, \vec{i}, \vec{j}, \vec{k})\) and such as the following figure:
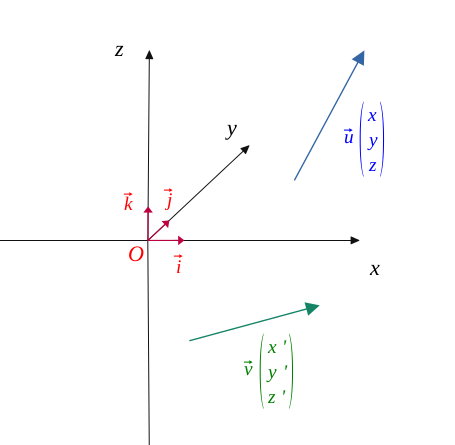
So, we can express \(\vec{u} \) and \(\vec{v} \) in the following formula:
$$ \Biggl \{ \begin{gather*}
\vec{u} = x \vec{i} + y \vec{j} +z \vec{k} \\
\vec{v} = x' \vec{i} + y' \vec{j} +z' \vec{k} \end{gather*} $$
Then, the scalar product \(\vec{u}.\vec{v} \) is worth:
$$ \vec{u}.\vec{v} = (x \vec{i} + y \vec{j} +z \vec{k}) . ( x' \vec{i} + y' \vec{j} +z' \vec{k}) $$
$$ \vec{u}.\vec{v} = xx'\vec{i}.\vec{i} + xy'\vec{i}.\vec{j} + xz'\vec{i}.\vec{k} + yx'\vec{j}.\vec{i} + yy''\vec{j}.\vec{j} + yz'\vec{j}.\vec{k} + zx'\vec{k}.\vec{i} + zy'\vec{k}.\vec{j} + zz'\vec{k}.\vec{k} $$
$$ \vec{u}.\vec{v} = xx' {|| \vec{i} ||}^2 + yy''{|| \vec{j} ||}^2 + zz'{|| \vec{k} ||}^2 + xy'\vec{i}.\vec{j} + xz'\vec{i}.\vec{k} + yx'\vec{j}.\vec{i} + yz'\vec{j}.\vec{k} + zx'\vec{k}.\vec{i} + zy'\vec{k}.\vec{j} \qquad (1) $$
The three vectors \(\vec{i},\vec{j}, \vec{k} \) are by hypothesis our unit vectors, then:
$$ {|| \vec{i} ||}^2 = {|| \vec{j} ||}^2 = {|| \vec{k} ||}^2 = 1 $$
Furthermore, being in an orthognal reference frame, the three vectors \(\vec{i},\vec{j}, \vec{k} \) are orthogonal, so their scalar product is zero:
$$ \vec{i}.\vec{j} = \vec{i}.\vec{k}= \vec{j}.\vec{k} = 0 $$
And by the commutative law of the scalar product, we do also have:
$$ \vec{j}.\vec{i} = \vec{k}.\vec{i}= \vec{k}.\vec{j} = 0 $$
Now, rewriting \((1) \),
$$ \vec{u}.\vec{v} = xx' + yy'' + zz' + \hspace{0.1em} \underbrace { xy'\vec{i}.\vec{j} + xz'\vec{i}.\vec{k} + yx'\vec{j}.\vec{i} + yz'\vec{j}.\vec{k} + zx'\vec{k}.\vec{i} + zy'\vec{k}.\vec{j} } _\text{ \(= \hspace{0.1em} 0\)} $$
Et finalement,
$$ \forall \left [\vec{u}\begin{pmatrix} x\\ y\\z \end{pmatrix} , \vec{v}\begin{pmatrix} x'\\ y'\\z' \end{pmatrix} \right], $$
$$ \vec{u}. \vec{v} = xx' + yy' +zz' $$
Let \((\lambda, \mu) \in \hspace{0.04em} \mathbb{R}^2\) be two real numbers, and \(\vec{u}\begin{pmatrix} x\\ y\\z \end{pmatrix}, \ \vec{v}\begin{pmatrix} x'\\ y'\\z' \end{pmatrix}\) two vectors.
Performing the scalar product \( (\lambda\vec{u}).\vec{v}\), we do have:
$$ (\lambda\vec{u}).\vec{v} = || \lambda \vec{u} || \times || \vec{v} || \times cos(\lambda \vec{u}, \vec{v}) $$
The norm \( || \lambda \vec{u} || \) of thevector \( \vec{\lambda u}\begin{pmatrix} \lambda x\\ \lambda y\\ \lambda z \end{pmatrix} \) is worth:
$$ || \lambda \vec{u} || = \sqrt{ (\lambda x)^2 + (\lambda y)^2 + (\lambda z)^2 }$$
$$ || \lambda \vec{u} || = \sqrt{ \lambda^2 (x^2 + y^2 + z^2) }$$
$$ || \lambda \vec{u} || = |\lambda| \times || \vec{u} ||$$
So,
$$ (\lambda\vec{u}).\vec{v} = |\lambda| \times || \vec{u} || \times || \vec{v} || \times cos(\lambda \vec{u}, \vec{v}) $$
Regarding the angle \( (\lambda \vec{u}, \vec{v}) \), it is no different from \( ( \vec{u}, \vec{v}) \), because \( ( \lambda \vec{u}) \) is only the extension of the vector \( \vec{u}\).
$$ (\lambda\vec{u}).\vec{v} = |\lambda| \times || \vec{u} || \times || \vec{v} || \times cos( \vec{u}, \vec{v}) $$
And as result,
$$ \forall \lambda \in \hspace{0.04em} \mathbb{R}, \ \forall (\vec{u}, \vec{v}),$$
$$ (\lambda\vec{u}).\vec{v} = |\lambda| \times \vec{u}. \vec{v}$$
By performing the same reasoning on the right-handed vector, we do obtain right linearity:
$$ \forall \lambda \in \hspace{0.04em} \mathbb{R}, \ \forall (\vec{u}, \vec{v}),$$
$$ \vec{u}.(\lambda\vec{v}) = |\lambda| \times \vec{u}. \vec{v}$$
And we then obtain bilinearity:
$$ \forall \lambda \in \hspace{0.04em} \mathbb{R}, \ \forall (\vec{u}, \vec{v}),$$
$$ (\lambda\vec{u}).\vec{v} = \vec{u}.(\lambda\vec{v}) = |\lambda| \times \vec{u}. \vec{v}$$
Furthermore, performing the scalar product \( (\lambda\vec{u}).(\mu\vec{v})\), we do obtain:
$$ \forall (\lambda, \mu) \in \hspace{0.04em} \mathbb{R}^2, \ \forall (\vec{u}, \vec{v}),$$
$$ (\lambda\vec{u}).(\mu\vec{v}) = |\lambda| \times |\mu| \times \vec{u}. \vec{v} $$
Let \(\vec{u}\), \(\vec{v}\) and \(\vec{w}\) be three vectors, also expressed \(\overrightarrow{AB}\), \(\overrightarrow{AC}\) and \(\overrightarrow{CD}\) such as the following figure:

We also note in this figure the sum \((\vec{v} + \vec{w})\) giving \(\overrightarrow{AD}\).
-
Right-hand distributivity
So the scalar product \(\vec{u}.( \vec{v} + \vec{w}) \) is worth :
$$ \vec{u}.( \vec{v} + \vec{w}) = || u || \times || v + w || \times cos(\vec{u}, \vec{v} + \vec{w})$$
$$ \vec{u}.( \vec{v} + \vec{w}) = || \overrightarrow{AB} || \times || \overrightarrow{AD} || \times cos(\overrightarrow{AB}, \overrightarrow{AD}) \qquad (1) $$
Let us now calculate what the scalar products are independently worth \(\vec{u}.\vec{v}\) and \(\vec{u}.\vec{w}\):
$$
\left \{ \begin{gather*}
\vec{u}.\vec{v} = || \overrightarrow{AB} || \times || \overrightarrow{AC} || \times cos(\overrightarrow{AB}, \overrightarrow{AC}) \\
\vec{u}.\vec{w} = || \overrightarrow{AB} || \times || \overrightarrow{CD} || \times cos(\overrightarrow{AB}, \overrightarrow{CD})
\end{gather*} \right \}
$$

But \(\left[|| \overrightarrow{AC} || \times cos(\overrightarrow{AB}, \overrightarrow{AC})\right]\) and \(\left[|| \overrightarrow{CD} || \times cos(\overrightarrow{AC}, \overrightarrow{CD})\right]\) are the respective orthogonal projections of vectors \(\overrightarrow{AC}\) and \(\overrightarrow{CD}\) on vector \(\overrightarrow{AB}\).
$$
\left \{ \begin{gather*}
\vec{u}.\vec{v} = || \overrightarrow{AB} || \times || \overrightarrow{AC'} || \qquad(2) \\
\vec{u}.\vec{w} = || \overrightarrow{AB} || \times || \overrightarrow{C'D'} || \qquad(3)
\end{gather*} \right \}
$$
So, the sum of the two expressions \((2)\) and \((3)\) is worth:
$$ \vec{u}.\vec{v} + \vec{u}.\vec{w} = || \overrightarrow{AB} || \times || \overrightarrow{AC'} || + || \overrightarrow{AB} || \times || \overrightarrow{C'D'} || $$
$$ \vec{u}.\vec{v} + \vec{u}.\vec{w} = || \overrightarrow{AB} || \times \left[ || \overrightarrow{AC'} || + || \overrightarrow{C'D'} || \right] $$
Moreover, both vectors \(|| \overrightarrow{AC'} ||\) and \(|| \overrightarrow{C'D'} ||\) being aligned, we have:
$$ \vec{u}.\vec{v} + \vec{u}.\vec{w} = || \overrightarrow{AB} || \times || \overrightarrow{AD'} || $$
And \(|| \overrightarrow{AD'} ||\) being the orthogonal projection of the vector \(\overrightarrow{AD}\) on \(\overrightarrow{AB}\), we now have:
$$ \vec{u}.\vec{v} + \vec{u}.\vec{w} = || \overrightarrow{AB} || \times || \overrightarrow{AD} || \times cos(\overrightarrow{AB}, \overrightarrow{AD}) $$
So, thanks to the previous expression \((1)\), we finally have that:
$$ \forall (\vec{u}, \vec{v}, \vec{w}), $$
$$ \vec{u}.( \vec{v} + \vec{w}) = \vec{u}.\vec{v} + \vec{u}.\vec{w} $$
-
Left-handed distributive law
And thanks to the commutative law of the scalar product, we do have the same thing to the left:
$$ (\vec{u} + \vec{v}) . \vec{w} = \vec{w} . (\vec{u} + \vec{v}) $$
Devlopping the expression with the right-handed distributive law:
$$ (\vec{u} + \vec{v}) . \vec{w} = \vec{w}.\vec{u} + \vec{w}.\vec{v} $$
And still with the commutative law:
$$ (\vec{u} + \vec{v}) . \vec{w} = \vec{u}.\vec{w} + \vec{v}.\vec{w} $$
And finally,
$$ \forall (\vec{u}, \vec{v}, \vec{w}), $$
$$ (\vec{u} + \vec{v}) . \vec{w} = \vec{u}.\vec{w} + \vec{v}.\vec{w} $$
We saw above that the scalar product is distributive, that is the property that will be used in this part.
-
Calculation of \( (\vec{u} + \vec{v})^2 \)
$$ (\vec{u} + \vec{v})^2 = (\vec{u} + \vec{v}).(\vec{u} + \vec{v}) $$
$$ (\vec{u} + \vec{v})^2 =\vec{u}. \vec{u} + \vec{u}.\vec{v} + \vec{u}.\vec{v} - \vec{v}. \vec{v} $$
$$ (\vec{u} + \vec{v})^2 = {|| \vec{u} ||}^2 + 2 \vec{u}.\vec{v} + {|| \vec{v} ||}^2 $$
-
Calculation of \( (\vec{u} - \vec{v})^2 \)
This is the same calculation but with a \((-)\) sign in the double product.
$$ (\vec{u} - \vec{v})^2 = (\vec{u} - \vec{v}).(\vec{u} - \vec{v}) $$
$$ (\vec{u} - \vec{v})^2 =\vec{u}. \vec{u} - \vec{u}.\vec{v} - \vec{u}.\vec{v} - \vec{v}. \vec{v} $$
$$ (\vec{u} - \vec{v})^2 = {|| \vec{u} ||}^2 - 2 \vec{u}.\vec{v} + {|| \vec{v} ||}^2 $$
-
Calculation of \( (\vec{u} + \vec{v}). (\vec{u} - \vec{v}) \)
$$ (\vec{u} + \vec{v}). (\vec{u} - \vec{v}) = \vec{u}. \vec{u} - \vec{u}. \vec{v} + \vec{v}. \vec{u} - \vec{v}. \vec{v} $$
We saw above that the scalar product is commutative, so \( \vec{u}. \vec{v} = \vec{v}. \vec{u} \), and:
$$ (\vec{u} + \vec{v}). (\vec{u} - \vec{v}) = {|| \vec{u} ||}^2 \hspace{0.1em} \underbrace{ - \ \vec{u}. \vec{v} + \vec{u}. \vec{v} } _\text{ \(= \hspace{0.1em} 0 \)} \hspace{0.1em} - {|| \vec{v} ||}^2$$
$$ {|| \vec{u} ||}^2 - {|| \vec{v} ||}^2= (\vec{u} + \vec{v}) (\vec{u} - \vec{v}) $$
As a result, we obtain the same formulas as the classical remarkable identities.
We saw above that:
$$ \Biggl \{ \begin{gather*}
(\vec{u} + \vec{v})^2 = {|| \vec{u} ||}^2 + 2 \vec{u}.\vec{v} + {|| \vec{v} ||}^2 \qquad (4) \\
(\vec{u} - \vec{v})^2 = {|| \vec{u} ||}^2 - 2 \vec{u}.\vec{v} + {|| \vec{v} ||}^2 \qquad (5)
\end{gather*} $$
Working with the expression \( (4) \), we do have:
$$ (\vec{u} + \vec{v})^2 = {|| \vec{u} ||}^2 + 2 \vec{u}.\vec{v} + {|| \vec{v} ||}^2 \qquad (4) $$
Then \( (4) \) becomes now:
$$ {|| \vec{u} + \vec{v} ||}^2 = {|| \vec{u} ||}^2 + 2 \vec{u}.\vec{v} + {|| \vec{v} ||}^2$$
$$ 2 \vec{u}.\vec{v} = {|| \vec{u} + \vec{v} ||}^2 - {|| \vec{u} ||}^2 - {|| \vec{v} ||}^2$$
And finally,
$$ \vec{u}.\vec{v} =\frac{1}{2} \left( {|| \vec{u} + \vec{v} ||}^2 - {|| \vec{u} ||}^2 - {|| \vec{v} ||}^2 \right ) $$
In the same way, working with the expression \( (5) \):
$$ (\vec{u} - \vec{v})^2 = {|| \vec{u} ||}^2 - 2 \vec{u}.\vec{v} + {|| \vec{v} ||}^2 $$
$$ {|| \vec{u} - \vec{v} ||}^2 = {|| \vec{u} ||}^2 - 2 \vec{u}.\vec{v} + {|| \vec{v} ||}^2 $$
$$ 2 \vec{u}.\vec{v} = {|| \vec{u} ||}^2 + {|| \vec{v} ||}^2 - {|| \vec{u} - \vec{v} ||}^2 $$
$$ \vec{u}.\vec{v} =\frac{1}{2} \left( {|| \vec{u} ||}^2 + {|| \vec{v} ||}^2 - {|| \vec{u} -\vec{v} ||}^2 \right ) $$
The scalar projection of \(\vec{u}\) onto \(\vec{v}\) is worth:
$$ || \hspace{0.1em} \vec{v'} || = || \vec{v} || \times cos(\vec{u}, \vec{v}) $$
Thus, having its standard we can attribute to it the direction and the sens of \(\vec{u}\) via the operation:
$$ \vec{v'} = || \hspace{0.1em} \vec{v'} || \times \frac{\vec{u}}{|| \vec{u} ||^2} $$
And with the above, we have:
$$ \vec{v'} = || \vec{v} || \times cos(\vec{u}, \vec{v}) \times \frac{\vec{u}}{|| \vec{u} ||} $$
$$ \vec{v'} = \textcolor{#606B9E}{ \frac{|| \vec{u} ||}{|| \vec{u} ||}} || \vec{v} || \times cos(\vec{u}, \vec{v}) \times \frac{\vec{u}}{|| \vec{u} ||} $$
$$ \vec{v'} = \vec{u}.\vec{v} \times \frac{\vec{u}}{|| \vec{u} ||^2} $$

$$ \forall (\vec{u}, \vec{v}), $$
The vectorial projection of \(\vec{u}\) onto \(\vec{v}\) is worth:
$$ \overrightarrow{proj}_{\mathcal{(\vec{u})}} \hspace{0.1em} \bigl(\vec{v}\bigr) = \frac{(\vec{u}.\vec{v})}{||\vec{u}||^2}. \vec{u} $$
Examples
-
Calculate a distance from a point to a plane
Let \((\mathcal{P})\) be a plane in space, passing through a point \(A(x_0, y_0, z_0)\) and orthogonal to a vector \(\vec{n}\begin{pmatrix} a\\ b \\c \end{pmatrix}\)(with \(a, b, c \) all three non-zero).
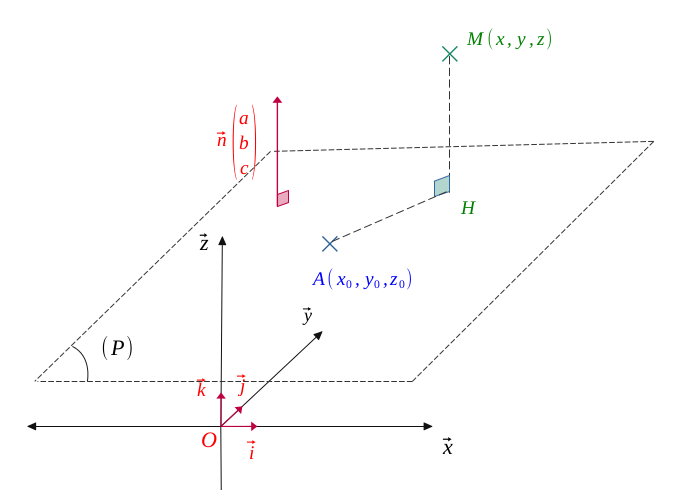
We need to determine the distance \([HM]\) from point \(M\bigl[x, y, z \bigr]\) to the plane \((\mathcal{P})\).
As both vectors \(\vec{n}\) and \(\overrightarrow{HA}\) are orthogonal, we do have:
$$ \vec{n} \ . \ \overrightarrow{HA} = 0$$
$$ \vec{n} \ . \ (\overrightarrow{HM} + \ \overrightarrow{MA}) = 0$$
$$ \vec{n} \ . \ \overrightarrow{HM} + \ \vec{n} \ . \ \overrightarrow{MA} = 0$$
$$ || \vec{n} || \times || \overrightarrow{HM} || + \vec{n} \ . \ \overrightarrow{MA} = 0$$
$$ || \overrightarrow{HM} || = \frac{\vec{n} \ . \ \overrightarrow{AM}}{ || \vec{n} ||} $$
$$ HM = \left | \frac{\vec{n} \ . \ \overrightarrow{AM}}{ || \vec{n} ||} \right| $$
Therefore, knowing the coordinates of point \(M\), we can apply the scalar product calculation by the coordinates product:
$$ HM = \left | \frac{a(x -x_0) + b(y-y_0) + c(z-z_0) }{ \sqrt{a^2 + b^2 + c^2}} \right| $$











 Go to the top of the page
Go to the top of the page