The properties of the binom\(: \binom{n}{p}\)
Let \((p,n) \in \hspace{0.04em}\mathbb{N}^2 \) be two natural numbers with \( p \leqslant n \).
We call \(\binom{n}{p} \) ("\( p \) among \( n \)") to number of ways to take \( p \) elements among a set of \( n \) elements.
We also call it the binom, and meets the following definition:
$$ \forall (p,n) \in \hspace{0.04em}\mathbb{N}^2, \enspace p \leqslant n, $$
$$ \binom{n}{p} = \frac{n \hspace{0.1em} !}{p \hspace{0.1em} ! \hspace{0.1em} (n-p) \hspace{0.1em} !} $$
$$ \forall n \in \mathbb{N}, $$
$$ \binom{n}{0} = \binom{n}{n} = 1$$
$$ \forall n \in \mathbb{N}, $$
$$ \binom{n}{1} = n $$
$$ \forall (p,n) \in \hspace{0.04em}\mathbb{N}^2, \enspace p \leqslant n, $$
$$ \binom{n}{p} = \binom{n}{n-p} $$
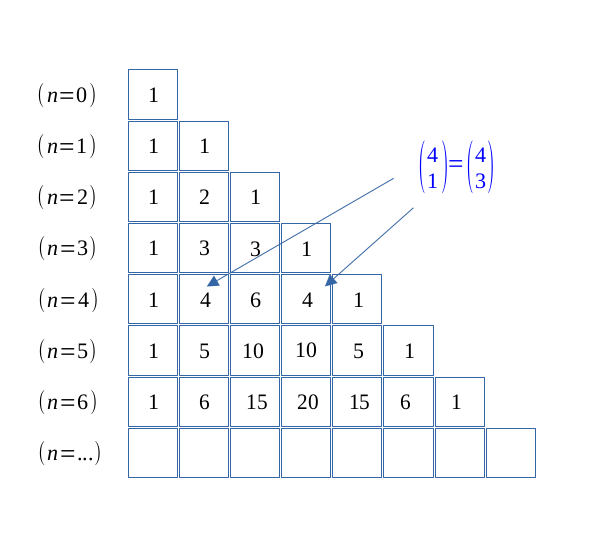
$$ \forall (p,n) \in \hspace{0.04em}\mathbb{N}^2, \enspace p \leqslant n, $$
$$ \binom{n}{p} = \frac{n}{p} \binom{n -1}{p-1} $$
$$ \forall (p,n) \in \hspace{0.04em}\mathbb{N}^2, \enspace p \leqslant n -1, $$
$$ \binom{n}{p} = \binom{n -1}{p -1 } + \binom{n - 1}{p} \qquad \text{(Pascal's formula)} $$
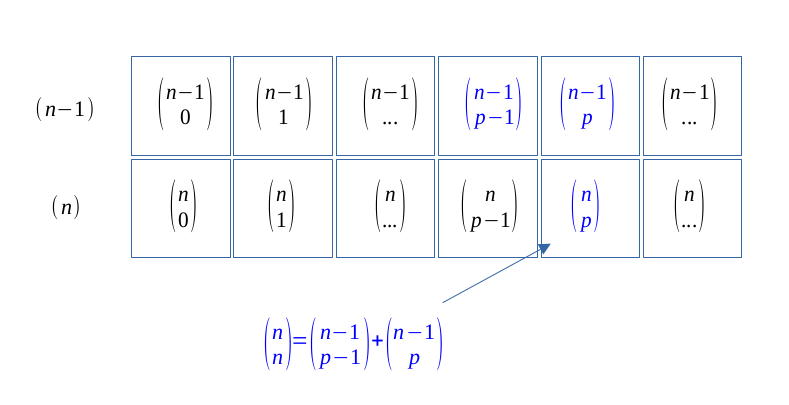
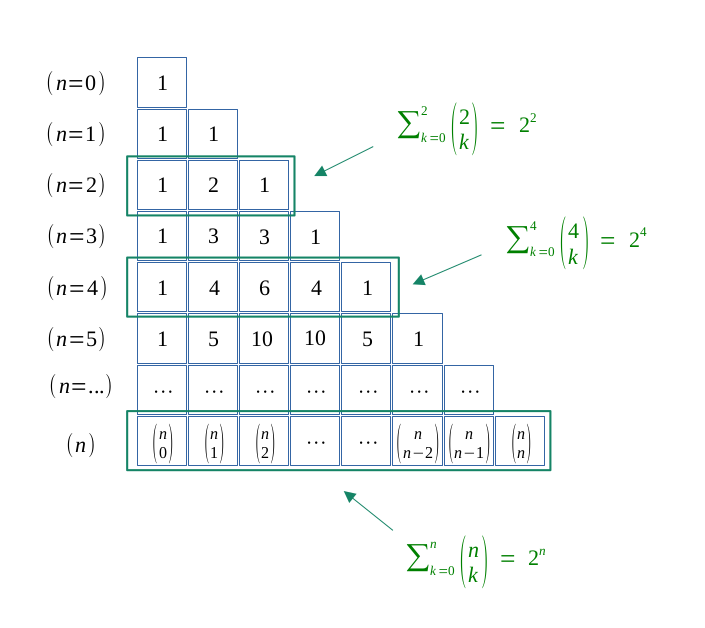
$$\forall n \in \mathbb{N}, $$
$$ \sum_{p = 0}^n \binom{n}{p} = \hspace{0.2em} 2^n $$
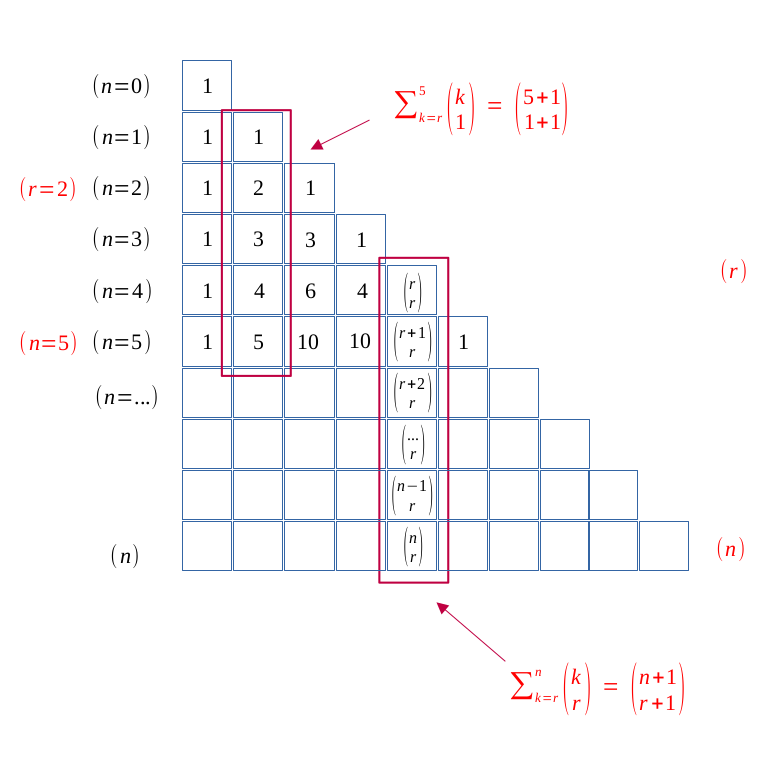
$$\forall (r, n) \in \hspace{0.04em}\mathbb{N}^2, \enspace r \leqslant n, $$
$$ \sum_{k=r}^n \binom{k}{r} = \binom{n+1}{r +1} $$
Demonstrations
Let \((p,n) \in \hspace{0.04em}\mathbb{N}^2 \) be two natural numbers.
There is only one way to take none or all elements in a \( n \) elements set.
Otherwise, by the binom's formula, we do have:
$$ \binom{n}{0} = \frac{n \hspace{0.1em} !}{0 \hspace{0.1em} ! \ n \hspace{0.1em} !} =1 $$
The same thing happen with \(n\), we do have:
$$ \binom{n}{n} = \frac{n \hspace{0.1em} !}{ n \hspace{0.1em} ! \ 0 \hspace{0.1em} ! } =1 $$
And finally,
$$ \forall n \in \mathbb{N}, $$
$$ \binom{n}{0} = \binom{n}{n} = 1$$
By the binom's formula, we do have:
$$ \binom{n}{1} = \frac{n \hspace{0.1em} !}{1! \ (n-1)!} =1 $$
$$ \binom{n}{1} = \frac{n (n-1)!}{1! \ (n-1)!} = n $$
And finally,
$$ \forall n \in \mathbb{N}, $$
$$ \binom{n}{1} = n $$
The Pascal's triangle definitely illustrates the symmetry between \( p\) and \( (n-p) \) elements among \(n\).

In addition, we can see by calculation that:
$$ \binom{n}{p} = \frac{n \hspace{0.1em} !}{p \hspace{0.1em} ! \hspace{0.1em} (n-p) \hspace{0.1em} !} $$
$$ \binom{n}{n-p} = \frac{n \hspace{0.1em} !}{ (n-p) \hspace{0.1em} ! (n - (n-p))!} = \frac{n \hspace{0.1em} !}{p \hspace{0.1em} ! \hspace{0.1em} (n-p) \hspace{0.1em} !}$$
So,
$$ \forall (p,n) \in \hspace{0.04em}\mathbb{N}^2, \enspace p \leqslant n, $$
$$ \binom{n}{p} = \binom{n}{n-p} $$
By the binom's formula, we do have:
$$ \binom{n}{p} = \frac{n \hspace{0.1em} !}{p \hspace{0.1em} ! \hspace{0.1em} (n-p) \hspace{0.1em} !} $$
$$ \binom{n}{p} = \frac{n(n-1)!}{p(p-1)! \hspace{0.1em} (n-p) \hspace{0.1em} !} $$
$$ \binom{n}{p} = \frac{n}{p} \frac{(n-1)!}{(p-1)! \hspace{0.1em} (n-p) \hspace{0.1em} !} $$
Now, we notice that for the denominator:
$$ n-p = (n-1) - (p-1) $$
Therefore,
$$ \binom{n}{p} = \frac{n}{p} \frac{(n-1)!}{(p-1)!((n-1) - (p-1))!} $$
$$ \binom{n}{p} = \frac{n}{p} \binom{n -1}{p-1} $$
As a result we do have,
$$ \forall (p,n) \in \hspace{0.04em}\mathbb{N}^2, \enspace p \leqslant n, $$
$$ \binom{n}{p} = \frac{n}{p} \binom{n -1}{p-1} $$
-
By visualising by the Pascal's triangle
To retrieve the Pascal's triangle, we add the each case's value with its left neighbor to find the upwards neighbor.
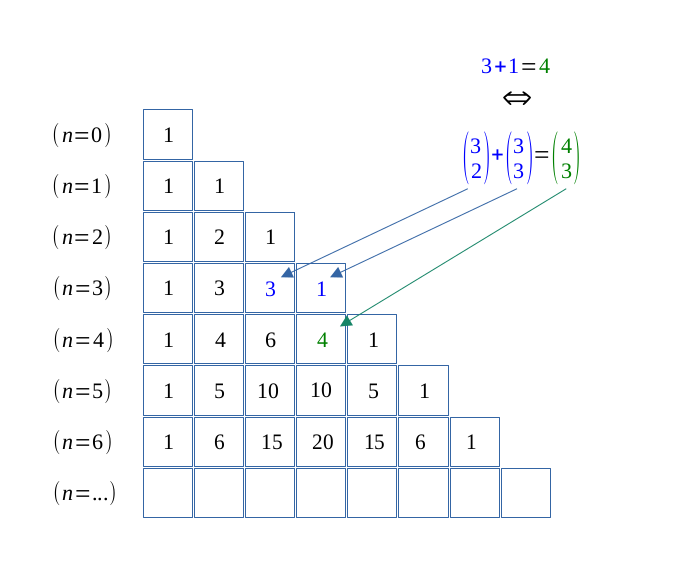
Moreover, if we consider the \( (n-1)\) and \(n\) ranks of the Pascal's triangle, the formula clearly appears.

By visualising we found out that,
$$ \forall (p,n) \in \hspace{0.04em}\mathbb{N}^2, \enspace p \leqslant n -1, $$
$$ \binom{n}{p} = \binom{n -1}{p -1 } + \binom{n - 1}{p} \qquad \text{(Pascal's formula)} $$
-
By reasoning
Let consider a \( E \) set containing \(n\) elements.
$$ E = \Bigl \{ e_1, e_2 , \hspace{0.2em} ... \hspace{0.2em}, e_{n} \Bigr \} $$
In this set, the number possible part containing \( p \) elements is \( \binom{n}{p} \).
Let split this set in two subsets: \( E_1 \) and \( E_2 \).
-
\( E_1\): a set of the possible parts of \( E \) which contains \( e_n \)
$$
E_1 =
\begin{Bmatrix}
\Bigl \{ e_1 , e_2, e_3, \ ... \ , e_n \Bigr \} \\
\Bigl \{ e_1 , e_3, e_4, \ ... \ , e_n \Bigr \} \\
\Bigl \{ e_1 , e_2, e_4, \ ... \ , e_n \Bigr \} \\
\Bigl \{................ \Bigr \} \\
\Bigl \{ \underbrace { e_1 , e_2, e_4, \ ... \ , e_n} _\text{ \(p\) elements } \Bigr \}
\\
\end{Bmatrix}
$$
Being said that all these parts contain\( e_n \), the \( E_1 \) set can be simplified:
$$
E_1 =
\begin{Bmatrix}
\Bigl \{ e_1 , e_2, e_3, \ ... \ , e_n \Bigr \} \\
\Bigl \{ e_1 , e_3, e_4, \ ... \ , e_n \Bigr \} \\
\Bigl \{ e_1 , e_2, e_4, \ ... \ , e_n \Bigr \} \\
\Bigl \{................ \Bigr \} \\
\Bigl \{ \underbrace { e_1 , e_2, e_4, \ ... \ , e_n} _\text{ \(p\) elements } \Bigr \}
\\
\end{Bmatrix}
\enspace
\Longrightarrow
\enspace
\begin{Bmatrix}
\Bigl \{ e_1 , e_2, e_3, \ ... \ \Bigr \} \\
\Bigl \{ e_1 , e_3, e_4, \ ... \ \Bigr \} \\
\Bigl \{ e_1 , e_2, e_4, \ ... \ \Bigr \} \\
\Bigl \{............. \Bigr \} \\
\Bigl \{ \underbrace { e_1 , e_2, e_4, \ .... } _\text{ \((p -1)\) elements } \Bigr \}
\\
\end{Bmatrix}
$$
Then, the number of elements of \( E_1 \) is reduced to the number of ways to take \( (p -1) \) elements among \( (n-1) \) elements in \( E\), that is to say \( \binom{n -1}{p -1} \).
-
\( E_2 \): a set of the possible parts of \( E \) which not contains \( e_n \)
$$
E_2 = \underbrace {
\begin{Bmatrix}
{ e_1 , e_2, e_3, \ ... } \\
{ e_1 , e_3, e_4, \ ... } \\
{ e_1 , e_2, e_4, \ ... } \\
{............. } \\
{ e_1 , e_2, e_4, \ ... } \\
\end{Bmatrix} }
_\text{ \(p\) elements }
$$
As \( E_2 \) does not contain \(e_n\), so there is a \( (n-1) \) elements choice left to take \( p \) elements in it. That is to say \( \binom{n -1}{p} \).
We thus showed that:
$$ \forall (p,n) \in \hspace{0.04em}\mathbb{N}^2, \enspace p \leqslant n -1, $$
$$ \binom{n}{p} = \binom{n -1}{p -1 } + \binom{n - 1}{p} \qquad \text{(Pascal's formula)} $$
-
By calculation
Let us calculate \( \binom{n -1}{p -1} + \binom{n -1}{p} \):
$$ \binom{n -1}{p -1} + \binom{n -1}{p} = \frac{(n-1) !}{ p \hspace{0.1em} ! \ (n-1-p)!} + \frac{(n-1) !}{ (p-1)! \ (n-1-(p-1))!} $$
$$ \binom{n -1}{p -1} + \binom{n -1}{p} = \frac{(n-1) !}{ p \hspace{0.1em} ! \ (n-1-p)!} + \frac{(n-1) !}{ (p-1)! \ (n-p) \hspace{0.1em} !} $$
Now, we have to make both terms on a common denominator:
$$ \binom{n -1}{p -1} + \binom{n -1}{p} = \frac{(n-1) ! \ \textcolor{#AF5F5F}{(n-p)}}{ p \hspace{0.1em} ! \ (n-1-p)! \ \textcolor{#AF5F5F}{(n-p)}} + \frac{(n-1) ! \ \textcolor{#AF5F5F}{p}}{ (p-1)! \ (n-p) \hspace{0.1em} ! \ \textcolor{#AF5F5F}{p}} $$
$$ \binom{n -1}{p -1} + \binom{n -1}{p} = \frac{(n-1) ! \ (n-p)}{ p \hspace{0.1em} ! (n-p) \hspace{0.1em} ! } + \frac{(n-1) ! \ p }{ p \hspace{0.1em} ! \ (n-p) \hspace{0.1em} !} $$
Then we factorize it:
$$ \binom{n -1}{p -1} + \binom{n -1}{p} = \frac{(n-1) ! \ (n-p + p)}{ p \hspace{0.1em} ! (n-p) \hspace{0.1em} ! } $$
$$ \binom{n -1}{p -1} + \binom{n -1}{p} = \frac{n \hspace{0.1em} !}{ p \hspace{0.1em} ! (n-p) \hspace{0.1em} ! } $$
$$ \binom{n -1}{p -1} + \binom{n -1}{p} = \binom{n}{p} $$
As a result we do have,
$$ \forall (p,n) \in \hspace{0.04em}\mathbb{N}^2, \enspace p \leqslant n -1, $$
$$ \binom{n}{p} = \binom{n -1}{p -1 } + \binom{n - 1}{p} \qquad \text{(Pascal's formula)} $$
Let \( n \in \mathbb{N}\) be a natural number.
We want to compute the \( \binom{n}{k} \) sum, from \( 0\) to \( n\).

-
With the Newton's binomal
The Newton's binomal tells us that:
$$\forall n \in \mathbb{N}, \enspace \forall (a, b) \in \hspace{0.04em} \mathbb{R}^2,$$
$$ (a + b)^n = \sum_{p = 0}^n \binom{n}{p} a^{n-p}b^p $$
Taking the values \( \{ a = 1, \enspace b = 1 \}\), we do have:
$$ \sum_{p = 0}^n \binom{n}{p} = (1 + 1)^n $$
And as a result,
$$\forall n \in \mathbb{N}, $$
$$ \sum_{p = 0}^n \binom{n}{p} = \hspace{0.2em} 2^n $$
So:
$$ \binom{n}{0} + \binom{n}{1} \enspace + ... + \enspace \binom{n}{n-1} + \binom{n}{n} = \hspace{0.02em} 2^n $$
-
By a recurrence
Let show that the following statement \((S_n)\) is true:
$$\forall n \in \mathbb{N}, $$
$$ \binom{n}{0} + \binom{n}{1} \enspace + ... + \enspace \binom{n}{n-1} + \binom{n}{n} = \hspace{0.02em} 2^n \qquad (S_n) $$
-
First terme calculation
Let verify if this is the case for the first term, that is to say when \( n = 0 \).
$$ \sum_{p = 0}^0 \binom{0}{p} = \binom{0}{0} = 1 $$
But,
$$ 2^0 = 1 $$
We definitely do have:
$$ \sum_{p = 0}^0 \binom{0}{p} = \hspace{0.2em} 2^0 $$
\((S_0)\) is true.
-
Heredity
Let \( k \in \mathbb{N} \) be a natural number.
Let us assume that the following statement \((S_k)\) is true for all \( k \).
$$ \binom{k}{0} + \binom{k}{1} \enspace + ... + \enspace \binom{k}{k} + \binom{k}{k} = \hspace{0.2em} 2^{k} \qquad (S_{k}) $$
And let verify if it is also the case for \((S_{k + 1})\).
$$ \binom{k + 1}{0} + \binom{k + 1}{1} \enspace + ... + \enspace \binom{k + 1}{k} + \binom{k + 1}{k + 1} = \hspace{0.2em} 2^{k + 1} \qquad (S_{k + 1}) $$
Let us calculate the right member of \(( S_{k + 1} ) \):
$$ \binom{k + 1}{0} + \binom{k + 1}{1} \enspace + ... + \enspace \binom{k + 1}{k} + \binom{k + 1}{k + 1} $$
But thanks to the Pascal's formula, we know that:
$$ \forall (p,n) \in \hspace{0.04em}\mathbb{N}^2, \enspace p \leqslant n -1, $$
$$ \binom{n}{p} = \binom{n - 1}{p - 1} + \binom{n - 1}{p} \qquad \text{(Pascal's formula)} $$
So also that:
$$ \binom{n + 1}{p + 1} = \binom{n}{p} + \binom{n}{p + 1} \qquad (Pascal^*) $$
$$ \textcolor{#606B9E}{\binom{k + 1}{0}} + \textcolor{#4A8051}{\binom{k + 1}{1}} + \textcolor{#AF5F5F}{ \binom{k + 1}{2}} \enspace + ... + \enspace \textcolor{#7C578A}{\binom{k + 1}{k}} + \textcolor{#606B9E}{\binom{k + 1}{k + 1}} $$
Then, thanks to \( (Pascal^*) \), we do have:
$$ \textcolor{#606B9E}{\binom{k + 1}{0}} + \textcolor{#4A8051}{\binom{k}{0} + \binom{k}{1}} + \textcolor{#AF5F5F}{\binom{k}{1} + \binom{k}{2}} \enspace + ... + \enspace \textcolor{#7C578A}{\binom{k}{k - 1} + \binom{k}{k}} + \textcolor{#606B9E}{\binom{k + 1}{k + 1}} $$
Now, the first term equals the second one.
$$ \binom{k + 1}{0} = \binom{k}{0} $$
As well, the last equals to the second to last one.
$$ \binom{k + 1}{k + 1} = \binom{k}{k} $$
That leads us to:
$$ \binom{k}{0} + \binom{k}{0} + \binom{k}{1} + \binom{k}{1} + \binom{k}{2} \enspace + ... + \enspace \binom{k}{k - 1} + \binom{k}{k} +\binom{k}{k} $$
And finally:
$$ 2 \left[ \binom{k}{0} + \binom{k}{1} + \binom{k}{2} \enspace + ... + \enspace \binom{k}{k - 1} + \binom{k}{k} \right] $$
But, our hypothesis was that:
$$ \binom{k}{0} + \binom{k}{1} \enspace + ... + \enspace \binom{k}{k-1} + \binom{k}{k} = \hspace{0.2em} 2^k \qquad (S_k) $$
Thus, we deduce from it that:
$$ \binom{k + 1}{0} + \binom{k + 1}{1} \enspace + ... + \enspace \binom{k + 1}{k} + \binom{k + 1}{k + 1} = \hspace{0.2em} 2 \times 2^{k} $$
So:
$$ \binom{k + 1}{0} + \binom{k + 1}{1} \enspace + ... + \enspace \binom{k + 1}{k} + \binom{k + 1}{k + 1} = \hspace{0.2em} 2^{k + 1} \qquad (S_{k+1}) $$
Therefore, \((S_{k + 1})\) is true.
-
Conclusion
The statement \((S_n)\) is true for its first terme \(n_0 = 0\) and it is hereditary from terms to terms for all \(k \in \mathbb{N}\).
By the recurrence principle, that statement is true for all \(n \in \mathbb{N}\).
We thus showed by recurrence that:
$$\forall n \in \mathbb{N}, $$
$$ \sum_{p = 0}^n \binom{n}{p} = \hspace{0.2em} 2^n $$

Let \( (r, n) \in \hspace{0.04em} \mathbb{N}^2\) be two natural numbers.
We want to calculalte the vertical sum of \( \binom{k}{r} \), from \( r\) until \( n\).

We know from the Pascal's formula, that:
$$ \forall (p,n) \in \hspace{0.04em}\mathbb{N}^2, \enspace p \leqslant n -1, $$
$$ \binom{n}{p} = \binom{n - 1}{p - 1} + \binom{n - 1}{p} \qquad \text{(Pascal's formula)} $$
But it can also be written as:
$$ \binom{n + 1}{p + 1} = \binom{n}{p} + \binom{n}{p + 1} \qquad (Pascal^*) $$
Therefore, replacing by what we want to calculate,
$$ \forall (r,k) \in \hspace{0.04em}\mathbb{N}^2, \enspace r +1 \leqslant k, \enspace \binom{k + 1}{r + 1} = \binom{k}{r} + \binom{k}{r + 1} $$
And,
$$ \binom{k}{r} = \binom{k + 1}{r + 1} - \binom{k}{r + 1} \qquad (1) $$
Performing the wished sum, we firstly extract the first term of it:
$$ \sum_{k=r}^n \binom{k}{r} = \binom{r}{r} + \sum_{k=r + 1}^n \binom{k}{r} $$
Now we can inject the value of \((1) \):
$$ \sum_{k=r}^n \binom{k}{r} = \binom{r}{r} + \sum_{k=r + 1}^n \Biggl[ \binom{k + 1}{r + 1} - \binom{k}{r + 1} \Biggr] $$
And we notice that we have a case of a telescopic sum, we then have after simplification:
$$ \sum_{k=r}^n \binom{k}{r} = \binom{r}{r} + \binom{n + 1}{r + 1} - \binom{r+1}{r + 1} $$
$$ \sum_{k=r}^n \binom{k}{r} = 1 + \binom{n + 1}{r + 1} - 1 $$
And finally,
$$\forall (r, n) \in \hspace{0.04em}\mathbb{N}^2, \enspace r \leqslant n, $$
$$ \sum_{k=r}^n \binom{k}{r} = \binom{n+1}{r +1} $$
















 Go to the top of the page
Go to the top of the page