Let \( f, g\) be two functions defined on an interval \( I = \bigl[a,b \bigr]\) and their respective derivative \( f', g'\) defined on \(]a , b [\).
Now, let \( \alpha \in \overset{-}{I}\cup{\{\infty\}} \) be a point or an extremity of \( I\); \( \alpha \) be a point or an extremity, it can be whatever value, including \( -\infty \) or \( +\infty \).
In order to calculate the limit in \( \alpha\) of a function under the form of a quotient presenting an indeterminate form of type \( \left[ \frac{0}{0} \right]\) or \( \left[ \frac{\pm \infty}{\pm \infty} \right]\), there may be an interest in using this method, with the aim of removing indeterminacy.
$$ \forall x \in I, \enspace \forall \alpha \in \overset{-}{I}\cup{\{\infty\}}, \enspace g(x) \neq 0, \hspace{0.2em} g'(x) \neq 0, $$
-
Indeterminate form of type [zero/zero]\(: \left[ \frac{0}{0} \right]\)
Let \( f, g\) be two functions defined on \( I = \bigl[a,b \bigr]\) and \( \alpha\) a point or an extremity of \( I\), and their respective derivative \( f', g'\) which are non-zero at the same time, and the following hypothesis \( (H) \):
$$ \Biggl \{ \begin{gather*}
\lim_{x \to \alpha} \ f(\alpha) = 0 \\
\lim_{x \to \alpha} \ g(\alpha) = 0 \end{gather*} \qquad (H) $$
If we want to calculate:
$$ \lim_{x \to \alpha} \enspace \frac{f(x)}{g(x)} $$
We end up with an indeterminate form of type \( \left[ \frac{0}{0} \right]\):
$$ \lim_{x \to \alpha} \enspace \frac{f(x)}{g(x)} = \left[ \frac{0}{0} \right] $$
Thanks to Cauchy's mean value theorem, we know that:
$$ \forall (f, g) \ continuous \ on \ \bigl[a,b \bigr]^2 \text{ and } derivables \ sur \ \bigl ]a,b \bigr[^2, $$
$$ \exists c \in \bigl ]a,b \bigr[, \enspace \frac{f'(c)}{g'(c)} = \frac{f(b) - f(a)}{g(b) - g(a)} $$
In our case,
$$ \forall x \in I, \enspace \exists c \in \hspace{0.04em} ]\alpha, x[, \enspace \frac{f'(c)}{g'(c)} = \frac{f(x) - f(\alpha)}{g(x) - g(\alpha)} \qquad (1) $$
But, with \( (H) \) the expression \( (1) \) becomes \( (2) \):
$$ \forall x \in I, \enspace \exists c \in \hspace{0.04em} ]\alpha, x[, \enspace \frac{f'(c)}{g'(c)} = \frac{f(x)}{g(x)} \qquad (2) $$
Now, applying the limit when \( x \to \alpha \):
$$ \forall x \in I, \enspace \exists c \in \hspace{0.04em} ]\alpha, x[, \ \lim_{x \to \alpha} \enspace \frac{f'(c)}{g'(c)} = \lim_{x \to \alpha} \enspace \frac{f(x)}{g(x)} = l \qquad (3)$$
Now, as \( \alpha < c < x\), we do have these two implications:
$$ x \to \alpha \Longrightarrow c \to \alpha \Longrightarrow c \to x $$
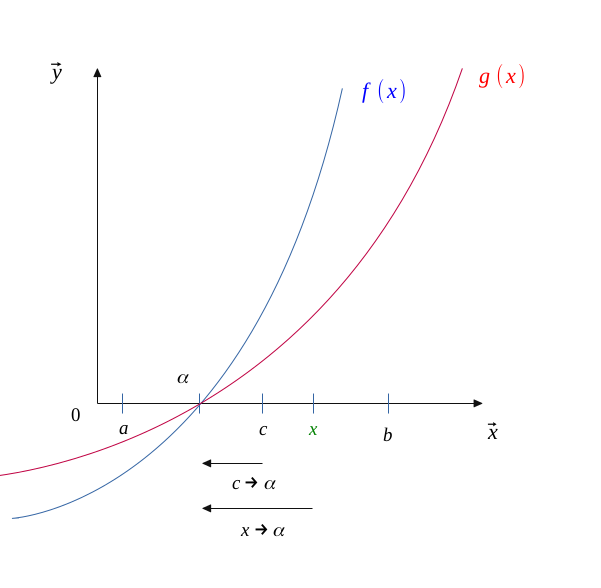
Therefore, if \( x \to \alpha \), then \( c \to x \) and we can rewrite \( (3) \) as \( (3') \) :
$$ \lim_{x \to \alpha} \enspace \frac{f'(x)}{g'(x)} = \lim_{x \to \alpha} \enspace \frac{f(x)}{g(x)} = l \qquad (3') $$
And as a result,
$$ \forall x \in I, \enspace \forall \alpha \in \overset{-}{I}\cup{\{\infty\}}, \enspace g(x) \neq 0, \hspace{0.2em} g'(x) \neq 0, $$
$$
\left \{ \begin{gather*}
\lim_{x \to \alpha} \ f(x) = 0, \\
\lim_{x \to \alpha} \ g(x) = 0 \\ \\
\lim_{x \to \alpha} \ \frac{f'(x)}{'g(x)} = l \end{gather*} \right \} \Longrightarrow \lim_{x \to \alpha} \enspace \frac{f(x)}{g(x)} = l \qquad \bigl(\text{L'Hôpital's rule} \bigr)
$$
-
Case 1 : removing indeterminacy
According to this rule, if: \( \lim_{x \to \alpha} \enspace f'(x) \neq 0 \) or even \( \lim_{x \to \alpha} \enspace g'(x) \neq 0 \), then, the limit of the quotient \( \frac{f}{g} \) can be easily obtained.
-
Case 2 : Still with indeterminacy
While we are still with an indeterminate form, we have to start the process again until the indeterminacy is removed.
-
Indeterminate form of type [infinite/infinite]\(: \left[ \frac{\pm \infty}{\pm \infty} \right]\)
In the same way, it can be shown that it also works when instead of \( (H)\) we do have a new hypothesis \( (H')\), such as:
$$ \Biggl \{ \begin{gather*}
\lim_{x \to \alpha} \enspace f(x) = \pm \infty \\
\lim_{x \to \alpha} \enspace g(x) = \pm \infty \end{gather*} \qquad (H') $$
Applying the limit, we then again have an indeterminate form:
$$ \lim_{x \to \alpha} \enspace \frac{f(x)}{g(x)} = \left[ \frac{\pm \infty}{\pm \infty} \right] $$
Let us rewrite \( (1) \) previously found:
$$ \forall x \in I, \enspace \exists c \in \hspace{0.04em} ]\alpha, x[, \enspace \frac{f'(c)}{g'(c)} = \frac{f(x) - f(\alpha)}{g(x) - g(\alpha)} \qquad (1) $$
Now, applying the limit when \( x \to \alpha \):
$$ \forall x \in I, \enspace \exists c \in \hspace{0.04em} ]\alpha, x[, \ \lim_{x \to \alpha} \enspace \frac{f'(c)}{g'(c)} = \lim_{x \to \alpha} \enspace \frac{f(x) - f(\alpha)}{g(x) - g(\alpha)}= l \qquad (4)$$
As \( f(\alpha) \) and \( g(\alpha) \) are both constants and knowing \( (H') \), we can write that:
$$ \lim_{x \to \alpha} \enspace \frac{f(x) - f(\alpha)}{g(x) - g(\alpha)} = \lim_{x \to \alpha} \ \frac{f(x)}{g(x)} = l \qquad (4') $$
So, thanks to \( (4) \) and \( (4') \) mixed together, we obtain \( (5)\):
$$ \forall x \in I, \enspace \exists c \in \hspace{0.04em} ]\alpha, x[, \ \lim_{x \to \alpha} \enspace \frac{f'(c)}{g'(c)} = \lim_{x \to \alpha} \enspace \frac{f(x)}{g(x)}= l \qquad (5)$$
Finally, in the same as above, we do have a chain reaction when \(x \to a\), such as:
$$ x \to \alpha \Longrightarrow c \to \alpha \Longrightarrow c \to x $$
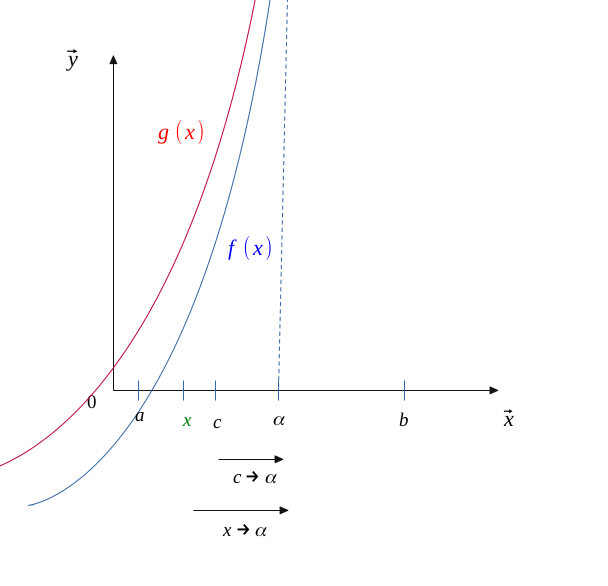
Therefore, if \( x \to \alpha \), then \( c \to x \) and we can rewrite \( (5) \) as \( (5') \) :
$$ \lim_{x \to \alpha} \enspace \frac{f'(x)}{g'(x)} = \lim_{x \to \alpha} \enspace \frac{f(x)}{g(x)} = l \qquad (5') $$
And as a result,
$$ \forall x \in I, \enspace \forall \alpha \in \overset{-}{I}\cup{\{\infty\}}, \enspace g(x) \neq 0, \hspace{0.2em} g'(x) \neq 0, $$
$$
\left \{ \begin{gather*}
\lim_{x \to \alpha} \ f(x) = \pm \infty, \\
\lim_{x \to \alpha} \ g(x) = \pm \infty \\ \\
\lim_{x \to \alpha} \ \frac{f'(x)}{g'(x)} = l \end{gather*} \right \} \Longrightarrow \lim_{x \to \alpha} \enspace \frac{f(x)}{g(x)} = l \qquad \bigl(\text{L'Hôpital's rule} \bigr)^*
$$
-
Indeterminate form of type [zero times infinite]\(: \bigl[ 0 \times \pm \infty \bigr]\)
At last, with a product \( fg \) having an indeterminate form of type \( [0] \times {[ \pm \infty]}\) applying the limit on \( \alpha\), such as:
$$ \lim_{x \to \alpha} \enspace f(x) g(x) = \bigl[ 0 \times \pm \infty \bigr]$$
$$ with \enspace \Biggl \{ \begin{gather*}
\lim_{x \to \alpha} \enspace f(x) = 0 \\
\lim_{x \to \alpha} \enspace g(x) = \pm \infty \end{gather*} $$
We can rather considerate the product as a quotient, to be able to apply the rule, so that:
$$ \lim_{x \to \alpha} \enspace f(x) g(x) = \lim_{x \to \alpha} \enspace \frac{f(x)}{\frac{1}{g(x)}}$$
-
Example 1
$$ \lim_{x \to 0^+} \enspace \frac{sin(x)}{x} = \left[ \frac{0^+}{0^+} \right] $$
We are facing an indeterminate form of type \( \left[ \frac{0}{0} \right]\).
Applying the rule, we do have:
$$ \lim_{x \to 0^+} \enspace \frac{sin(x)}{x} = \lim_{x \to 0} \enspace \frac{cos(x)}{1}= 1 $$
-
Example 2
$$ \lim_{x \to +\infty} \enspace \frac{e^x}{x^n} = \left[ \frac{+ \infty}{+ \infty} \right] $$
Applying the rule in chain, the numerator will remain fixed, but the denominator will become a constant over the \(n\)-th derivation:
$$ \lim_{x \to +\infty} \enspace \frac{e^x}{x^n} = \lim_{x \to +\infty} \enspace \frac{e^x}{nx^{n-1}} $$
$$ \lim_{x \to +\infty} \enspace \frac{e^x}{x^n} = \lim_{x \to +\infty} \enspace \frac{e^x}{n(n-1)x^{n-2}} $$
$$ \lim_{x \to +\infty} \enspace \frac{e^x}{x^n} \enspace = \enspace... \enspace = \enspace \lim_{x \to +\infty} \enspace \frac{e^x}{n!} = + \infty $$
-
Example 3
$$ \lim_{x \to 0^+} \ x^n ln(x) = \bigl[ 0^+ \times - \infty \bigr] $$
$$ with \enspace \Biggl \{ \begin{gather*}
\lim_{x \to 0^+} \ x^n = \ 0^+ \\
\lim_{x \to 0^+} \ ln(x) = - \infty \end{gather*} $$
To apply the rule, let us considerate a quotient to calculate the limit:
$$ \lim_{x \to 0^+} \ x^n ln(x) = \lim_{x \to 0^+} \ \frac{ln(x)}{x^{-n}} $$
At this stage, applying the rule we do have:
$$ \lim_{x \to 0^+} \ x^n ln(x) = \lim_{x \to 0^+} \ \frac{1 \over x}{-nx^{-n-1}} $$
$$ \lim_{x \to 0^+} \ x^n ln(x) = \lim_{x \to 0^+} \ \frac{1}{-nx^{-n}} $$
$$ \lim_{x \to 0^+} \ x^n ln(x) = \lim_{x \to 0^+} \ - \frac{x^{n}}{n} = \ 0^+ $$
-
Example 4
$$ \lim_{x \to 0^+} \ \frac{ln(1 + x)}{x} = \left[ \frac{0^+}{0^+} \right] $$
$$ \lim_{x \to 0^+} \ \frac{ln(1 + x)}{x} = \lim_{x \to 0^+} \ \frac{\frac{1}{1 + x}}{1} = 1 $$
-
Example 5
$$ \lim_{x \to 0^+} \ \frac{e^x - 1}{x} = \left[ \frac{0^+}{0^+} \right] $$
$$ \lim_{x \to 0^+} \ \frac{e^x - 1}{x} = \lim_{x \to 0^+} \ \frac{e^x}{1} = 1 $$






 Go to the top of the page
Go to the top of the page