Formulas for calculating the area of a triangle
In the context of any triangle \(\{a, b, c\}\), with each angle opposite its length respectively, such that:
$$ \left \{ \begin{gather*}
\alpha \enspace opposé \enspace à \enspace a \\
\beta \enspace opposé \enspace à \enspace b \\
\gamma \enspace opposé \enspace à \enspace c \end{gather*} \right \} $$
And such as the following figure:
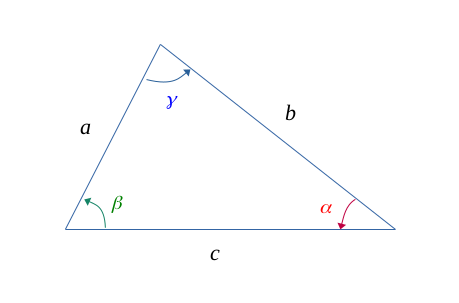
Area formula
The area formula tells us that:
$$\forall (a, b, c) \in \hspace{0.05em} \mathbb{R}^3, \enspace (\alpha, \beta, \gamma) \in \hspace{0.05em} \mathbb{R}^3, $$
Héron's formula
Héron's formula tells us that:
$$\forall (a, b, c) \in \hspace{0.05em} \mathbb{R}^3,$$
$$ S_{abc} = \sqrt{p(p-a)(p-b)(p-c)} \qquad (Héron) $$
$$ avec \enspace \Biggl \{ \begin{gather*}
p : half\hspace{-0.3em}-\hspace{-0.3em}perimeter \ of \ a \ triangle \\
p = \frac{a+b+c}{2}
\end{gather*} $$
Demonstrations
Area formula
To demonstrate this, let's project a height \( h_c \) along the length \( c \), and such as the following figure:
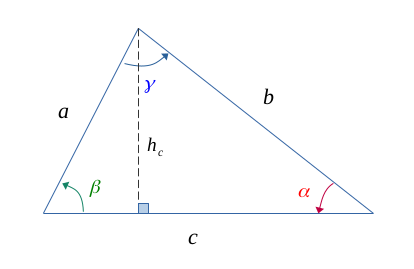
Immediately, the following relationships come:
As a result, it follows that:
But, the formula for the area of any triangle \(\{a, b, c\}\) is worth:
$$ S_{abc} = \frac{1}{2}c.h_c \qquad (\mathcal{A}) $$
Now, by injecting the values of \(h_c\) coming from \((1')\) and \((2')\) in that of \((\mathcal{A})\), we obtain the double equality:
Finally, by projecting one of the other two heights, we find the third equality, and finally:
$$\forall (a, b, c) \in \hspace{0.05em} \mathbb{R}^3,$$
Héron's formula
To demonstrate this formula, we project the height \( h_c \) as before along the length \( c \):

Thanks to Al-Kashi's theorem, we have the following relationship:
$$ a^2 + b^2 - 2ab.cos(\gamma) = c^2 $$
$$ a^2 + b^2 - c^2 = 2ab.cos(\gamma) $$
And then,
$$ \frac{a^2 + b^2 - c^2}{2ab} = cos(\gamma) \qquad (3) $$
But, we know that:
$$ sin^2(\gamma) = 1 - cos^2(\gamma) $$
$$ sin^2(\gamma) = \bigl(1 - cos(\gamma)\bigr)\bigl(1 + cos(\gamma)\bigr) \qquad (4) $$
Now injecting the expression \((3)\) into the expression \((4)\), we do have this:
$$ sin^2(\gamma) = \left(1 - \frac{a^2 + b^2 - c^2}{2ab} \right)\left(1 + \frac{a^2 + b^2 - c^2}{2ab}\right) $$
$$ sin^2(\gamma) = \left(\frac{2ab}{2ab} - \frac{a^2 + b^2 - c^2}{2ab} \right)\left(\frac{2ab}{2ab} + \frac{a^2 + b^2 - c^2}{2ab}\right) $$
$$ sin^2(\gamma) = \left(\frac{2ab - (a^2 + b^2 - c^2)}{2ab} \right)\left(\frac{2ab + (a^2 + b^2 - c^2) }{2ab}\right) $$
$$ sin^2(\gamma) = \left(\frac{2ab - a^2 - b^2 + c^2}{2ab} \right)\left(\frac{2ab + a^2 + b^2 - c^2 }{2ab}\right) $$
Arranging both parenthesis in order to obtain remarkable identities:
$$ sin^2(\gamma) = \left(\frac{-(a^2 + b^2 - 2ab) + c^2}{2ab} \right)\left(\frac{a^2 + b^2 + 2ab - c^2 }{2ab}\right) $$
$$ sin^2(\gamma) = \left(\frac{c^2 -(a-b)^2}{2ab} \right)\left(\frac{(a+b)^2 - c^2 }{2ab}\right) $$
We now factorize to obtain the third remarkable identity:
$$ sin^2(\gamma) = \left(\frac{\bigl(c - (a-b)\bigr)\bigl(c + (a-b)\bigr)}{2ab} \right)\left(\frac{ \bigl((a+b) -c \bigr)\bigl((a+b) + c \bigr)}{2ab}\right) $$
We remove the parentheses:
$$ sin^2(\gamma) = \left(\frac{(c-a+b)(c+a-b) }{2ab} \right)\left(\frac{ (a+b-c)(a+b+c) }{2ab}\right)$$
$$ sin^2(\gamma) = \frac{(c-a+b)(c+a-b)(a+b-c)(a+b+c)}{4a^2b^2} \qquad (5) $$
Moreover, we have seen more with the area formula that:
$$ S_{abc} = \frac{1}{2}ab . sin(\gamma) $$
And then also that:
$$ (S_{abc})^2 = \frac{1}{4}a^2b^2 . sin^2(\gamma) \qquad (6)$$
So, by injecting the expression \((5)\) into the expression \((6)\), we do have:
$$ (S_{abc})^2 = \frac{1}{4}a^2b^2 . \frac{(c-a+b)(c+a-b)(a+b-c)(a+b+c)}{4a^2b^2}$$
Putting the elements in order, we now have:
$$ (S_{abc})^2 = \frac{1}{16}(a+b+c) (a+b-c)(b+c-a)(a+c-b) $$
At this stage, let us introduce the perimeter \(P\) of the triangle, then the expression becomes:
$$ (S_{abc})^2 = \frac{1}{16}P (P - 2c)(P - 2a)(P - 2b) $$
Then that of half-perimeter \(p\) :
$$ (S_{abc})^2 = \frac{1}{16}2p (2p - 2c)(2p - 2a)(2p - 2b) $$
We factorize all expressions in parentheses by \(2\):
$$ (S_{abc})^2 = \frac{1}{16} \times 2p \times 2(p - c) \times 2(p - a) \times 2(p - b) $$
$$ (S_{abc})^2 = p (p - c)(p - a)(p - b) $$
And finally,
$$\forall (a, b, c) \in \hspace{0.05em} \mathbb{R}^3,$$
$$ S_{abc} = \sqrt{p(p-a)(p-b)(p-c)} \qquad (Héron) $$
$$ avec \enspace \Biggl \{ \begin{gather*}
p : half\hspace{-0.3em}-\hspace{-0.3em}perimeter \ of \ a \ triangle \\
p = \frac{a+b+c}{2}
\end{gather*} $$