Index
Let be two natural numbers \( (a, b) \in \hspace{0.04em}\mathbb{N}^2, \enspace a > b \).
Euclid's algorithm tells us that:
-
If \( b \) divides \( a \)
$$ \exists q \in \mathbb{N}, $$$$ b / a \ \Longrightarrow \ a = bq \ \Longrightarrow \ PGCD(a, b) = b $$
-
If \( b\) does not divide \( a\)
$$ \exists q \in \mathbb{N}, \enspace \exists R \in [\![0, (b-1) ]\!] , $$$$ b \nmid a \ \Longrightarrow \ a = bq + R $$
The \( GCD(a, b) \) is the last non-zero \( R_n \) of the Euclidian division of \( a \) by \( b \) such as:
$$ a = \textcolor{rgb(225 98 98)}{b} q_0 + \textcolor{rgb(73 174 65)}{R_0} $$As long as the remainder does not divide the previous division divisor , we continue the algorithm.
We then decompose the new element at each step:
$$ b = \textcolor{rgb(225 98 98)}{R_0} q_1 + \textcolor{rgb(73 174 65)}{R_1} \ \Longrightarrow \ R_0 = \textcolor{rgb(225 98 98)}{R_1} q_2 + \textcolor{rgb(73 174 65)}{R_2} \ \Longrightarrow \ R_k = \textcolor{rgb(225 98 98)}{R_{k + 1}} q_{k + 2} + \textcolor{rgb(73 174 65)}{R_{k + 2}} $$$$ up \ to \ \Longrightarrow R_{n - 3} = q_{n -1 }\textcolor{rgb(225 98 98)}{R_{n - 2}} + \textcolor{rgb(73 174 65)}{R_{n -1}} $$As long a the remainder \( R_{n - 1} \) still does not divide \( R_{n - 2} \), the remainder \( R_{n - 2} \) can be written:
$$ R_{n - 2} = q_{n}\textcolor{rgb(225 98 98)}{R_{n - 1}} + \textcolor{rgb(73 174 65)}{R_{n}} $$Until the moment where finally \( R_n \) divides \( R_{n - 1} \), so \( R_{n - 1} \) will be written:
$$ R_{n - 1} = q_{n + 1}\textcolor{rgb(225 98 98)}{R_{n}} $$At this stage, as we trace back the algorithm injecting each previous step's values until \( a \) and \( b \), we realize that we can always factorize by \(R_{n} \). Thus:
$$ GCD(a, b) = R_{n} $$\( \forall n \in \mathbb{N}\), \(\forall k \in [\![0, n ]\!] \), as long as the remainder \(R_{k} \) does not divide its predecessor \(R_{k -1 } \):
$$ a \nmid b \Longrightarrow GCD(a, b) = GCD(b, R_0) = GCD(R_0, R_1) = \enspace ... \enspace = GCD(R_{n - 1}, R_n) = R_n \neq 0$$
Proofs
Let be two integers \( (a, b) \in \hspace{0.04em} \mathbb{N}^2 \), with \( a > b \).
-
If \( b \) divides \( a \)
Then, \( a \) can be written:
$$ a = bq_0 \qquad (a) $$At this stage, as \( b /a \) and \( b/b \), so \( PGCD(a, b) = b\).
$$ \exists q \in \mathbb{N}, $$$$ b / a \ \Longrightarrow \ a = bq \ \Longrightarrow \ PGCD(a, b) = b $$ -
If \( b \) does not divide \( a \)
In this case, \( a \) can be written as:
$$ \exists q_0 \in \mathbb{N}, \enspace \exists R_0 \in [\![0, (b-1) ]\!] , \enspace a = \textcolor{rgb(225 98 98)}{b}q_0 + \textcolor{rgb(54 152 46)}{R_0} \qquad (a^*) $$So in a general way,
$$ \exists q \in \mathbb{N}, \enspace \exists R \in [\![0, (b-1) ]\!] , $$$$ b \nmid a \ \Longrightarrow \ a = bq + R $$-
If \( R_0 \) divides \( b \)
Then \( b \) can be written as:
$$ \exists q_1 \in \mathbb{N}, \enspace b = q_1R_0 \qquad (b) $$We can reassemble the algorithm and inject \( (b) \) into \( (a^*) \):
$$ a = bq_0 + R_0 = q_1R_0q_0 + R_0 = R_0 \underbrace{(q_1 q_0 + 1)} _\text{ \( Q_{a} \in \mathbb{N} \)} $$So,
$$ a = Q_{a}R_0 \qquad (a') $$We then have,
$$ \Biggl \{ \begin{gather*} a = Q_{a}R_0 \qquad (a') \\ b = q_1R_0 \qquad (b) \end{gather*} $$Ant at that moment, as \( R_0 /a \), \( R_0/b \) and \( R_0/R_0 \), so:
$$ GCD(a, b) =GCD(b, R_0) = R_0 $$ -
If \( R_0 \) does not divide \( b \)
In this case, \( b \) can be written as:
$$ \exists q_1 \in \mathbb{N}, \enspace \exists R_1 \in [\![0, (R_0-1) ]\!], \enspace b = \textcolor{rgb(225 98 98)}{R_0} q_1 + \textcolor{rgb(73 174 65)}{R_1} \qquad (b^*) $$-
if \( R_1 \) divides \( R_0 \)
Then \( R_0 \) can be written:
$$ \exists q_2 \in \mathbb{N}, \enspace R_0 = q_2R_1 \qquad (R_0) $$We can reassemble the algorithm and inject \( (R_0) \) into \( (b^*) \):
$$ b = R_0 q_1 + R_1 = q_2R_1 q_1 + R_1 = R_1 \underbrace{(q_2 q_1 + 1)} _\text{ \( Q_{b} \in \mathbb{N} \)} $$So,
$$ b = Q_{b}R_1 \qquad (b') $$We trace back the algorithm another time injecting the new value of \( (b') \) and \( (R_0) \) into \( (a^*) \):
$$a = bq_0 + R_0 = Q_{b}R_1q_0 + q_2R_1 = R_1 \underbrace{(Q_{b} q_0 + q_2)} _\text{ \( Q_{a} \in \mathbb{N} \)} $$$$a = Q_{a}R_1 \qquad (a') $$We then have,
$$ \Biggl \{ \begin{gather*} a = Q_{a}R_1 \qquad (a') \\ b = Q_{b}R_1 \qquad (b') \end{gather*} $$Now, as \( R_1 /a \), \( R_1/b \), \( R_1/R_0 \) and \( R_1/R_1 \), so:
$$ GCD(a, b) =GCD(b, R_0) =GCD(R_0, R_1) = R_1 $$ -
if \( R_1 \) does not divide \( R_0 \)
In this cas, \( R_0 \) can be written as:
$$ \exists q_2 \in \mathbb{N}, \enspace \exists R_2\in [\![0, (R_1-1) ]\!], \enspace R_0 = \textcolor{rgb(225 98 98)}{R_1} q_2 + \textcolor{rgb(73 174 65)}{R_2} \qquad (R_0^*) $$We continue the algorithm this way until \( R_n \) divides \( R_{n- 1} \) and then:
$$ R_{n - 1} = q_{n + 1}\textcolor{rgb(225 98 98)}{R_n} $$Thus, by tracing back the algorithm we get:
$$ R_{n - 2} = q_{n} \textcolor{rgb(225 98 98)}{R_{n - 1}} + \textcolor{rgb(73 174 65)}{R_n} $$$$ R_{n - 2} = q_{n}\textcolor{rgb(225 98 98)}{q_{n + 1}R_n} + \textcolor{rgb(73 174 65)}{R_n} = R_n\underbrace{(q_{n}q_{n + 1} + 1)} _ \text{ \( Q_{n - 2} \in \mathbb{N} \) } $$$$ R_{n - 2} = R_nQ_{n - 2} $$As a result, we have a chain reaction until the beginning of the algorithm:
$$ \Biggl[ R_{n - 3} = R_nQ_{n - 3} \Biggr] \Longrightarrow ... \Longrightarrow \Biggl[ R_{n - k} = R_nQ_{n - k} \Biggr] \Longrightarrow ... \Longrightarrow \Biggl[ R_{2} = R_nQ_{2} \Biggr] $$$$ \Biggl[ R_{1} = R_nQ_{1}\Biggr] \Longrightarrow \Biggl[ R_{0} = R_nQ_{0} \Biggr] \Longrightarrow \Biggl[ b = R_nQ_{b}\Biggr] \Longrightarrow \Biggl[ a = R_nQ_{a}\Biggr] $$\( R_n \) will be the greatest common divisor of all these numbers.
$$ GCD(a, b) = GCD(b, R_0) = GCD(R_0, R_1) = \enspace ... \enspace = GCD(R_{n - 1}, R_n) = R_n \neq 0$$
-
-
And finally,
\( \forall n \in \mathbb{N}\), \(\forall k \in [\![0, n ]\!] \), \tant que le reste \(R_{k} \) ne divise pas le reste \(R_{k -1 } \):
This remainder \( R_n \) can itself be broken into different factors, which will make up the set of divisors of \( a \) and \( b \):
Examples
-
Calculation of \( GCD(1365, 25) \)
We have seen that it is necessary to carry out successive divisions, in order to recover the last non-zero remainder of this division series.
-
Calculation of \( 1365 / 25 \)
\( 25 \) does not divide \( 1365 \), because there is a remainder. We first recover its floor .
$$ \left \lfloor{\frac{1365}{25}} \right \rfloor = 54 \hspace{5em} (1^{st} \ division) $$$$ \hspace{0.8em } \textcolor{#6187B2}{ \overset{\LARGE\frown}{1 \ 36} }5 $$$$ \textcolor{rgb(225 98 98)}{25} $$$$ \hspace{-0.2em } -1 \ 25 \hspace{0.04em} . \hspace{0.2em} $$$$ 54 $$$$ \hspace{-0.4em } = \textcolor{#6187B2}{ \overset{\LARGE\frown}{115}} $$$$ \hspace{-0.2em } -100 $$$$ \hspace{-0.2em } = \textcolor{rgb(73 174 65)}{15} $$So \( 1365 \) can be written:
$$ 1365 = \textcolor{rgb(225 98 98)}{25} \times 54 + \textcolor{rgb(73 174 65)}{15} $$Let's calculate the remainder \( \textcolor{rgb(73 174 65)}{R_0} \).
$$ 1365 -\textcolor{rgb(225 98 98)}{25} \times 54 = \textcolor{rgb(73 174 65)}{15} \hspace{5em} (R_0) $$So,
$$ 1365 = \textcolor{rgb(225 98 98)}{25} \times 54 + \textcolor{rgb(73 174 65)}{15} \qquad (a) $$$$ (a = \textcolor{rgb(225 98 98)}{b} q_0 + \textcolor{rgb(73 174 65)}{R_0}) $$ -
Calculation of \( 25 / 15 \)
\( 15 \) does not divide \( 25 \).
$$ \left \lfloor{\frac{25}{15}} \right \rfloor = 1 \hspace{5em} (2^{nd} \ division) $$$$ \hspace{0.8em } \textcolor{#6187B2}{ \overset{\LARGE\frown}{25} } $$$$ \textcolor{rgb(225 98 98)}{15} $$$$ -15 $$$$ 1 $$$$ \hspace{-0.2em } = \textcolor{rgb(73 174 65)}{10} $$Well \( 25 \) can be written:
$$ 25 = \textcolor{rgb(225 98 98)}{15} \times 1 + \textcolor{rgb(73 174 65)}{10} \qquad (b) $$$$ (b = \textcolor{rgb(225 98 98)}{R_0} q_1 + \textcolor{rgb(73 174 65)}{R_1}) $$ -
Calculation of \( 15 / 10 \)
\( 10 \) does not divide \( 15 \).
$$ \left \lfloor{\frac{15}{10}} \right \rfloor = 1 \hspace{5em} (3^{rd} \ division) $$$$ \hspace{0.8em } \textcolor{#6187B2}{ \overset{\LARGE\frown}{15} } $$$$ \textcolor{rgb(225 98 98)}{10} $$$$ -10 $$$$ 1 $$$$ \hspace{0.2em } = \textcolor{rgb(73 174 65)}{5} $$Then \( 15 \) can be written:
$$ 15 = \textcolor{rgb(225 98 98)}{10} \times 1 + \textcolor{rgb(73 174 65)}{5} \qquad (R_0) $$$$ (R_0 = \textcolor{rgb(225 98 98)}{R_1} q_2 + \textcolor{rgb(73 174 65)}{R_2}) $$ -
Calculation of \( 10 / 5 \)
Now, \( 5 \) divides \( 10 \). The remainder is zero.
$$ \frac{10}{5} = 2 \hspace{5em} (4^{th} \ division) $$$$ \hspace{0.8em } \textcolor{#6187B2}{ \overset{\LARGE\frown}{10} } $$$$ \textcolor{rgb(225 98 98)}{5} $$$$ -10 $$$$ 2 $$$$ \hspace{0.2em } = \textcolor{rgb(73 174 65)}{0} $$Then \( 10 \) can be written:
$$ 10 = \textcolor{rgb(225 98 98)}{5} \times 2 \qquad (R_1) $$$$ (R_1 = \textcolor{rgb(225 98 98)}{R_2} q_3) $$We therefore have a final result:
$$ GCD(1365, 25) = 5 $$$$ (GCD(a, b) = R_2) $$
-
-
Algorithm feedback
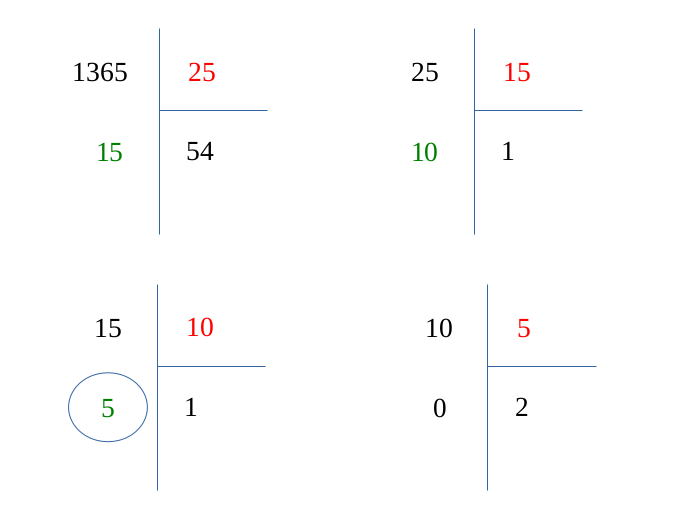
We can eventually go back through the algorithm and find two nuumbers that fit the Bézout's identity .
This theorem tell us thtat:
$$ \forall (a, b) \in \hspace{0.04em}\mathbb{N}^2, \enspace a > b, $$$$ \delta = a \wedge b \hspace{0.2em} \Longrightarrow \hspace{0.2em} \exists (u, v) \in \hspace{0.04em}\mathbb{Z}^2, \enspace au + bv = \delta \qquad (Bachet-Bézout)$$To do this, we will each time reinject the values into the result of the previous calculation.
$$ \Biggl \{ \begin{gather*} \underline{10} \hspace{0.1em} = \textcolor{rgb(225 98 98)}{5} \times 2 \qquad (R_1) \\ 15 = \hspace{0.1em} \underline{\textcolor{rgb(225 98 98)}{10}} \hspace{0.1em} \times 1 + \textcolor{rgb(73 174 65)}{5} \qquad (R_0) \end{gather*} \enspace \Longrightarrow \enspace 15 = \textcolor{rgb(225 98 98)}{(5 \times 2)} \times 1 + \textcolor{rgb(73 174 65)}{5} \qquad (R_0') $$We isolate the \( GCD \) value, because this is what we want in the end as a result.
$$ 15 = \textcolor{rgb(225 98 98)}{10} \times 1 + \textcolor{rgb(73 174 65)}{5} \qquad (R_0) \enspace \Longleftrightarrow \enspace \textcolor{rgb(73 174 65)}{5} = 15 - \textcolor{rgb(225 98 98)}{10} \times 1 \qquad (R_2) $$Then, we do have this:
$$ 25 = \textcolor{rgb(225 98 98)}{15} \times 1 + \textcolor{rgb(73 174 65)}{10} \qquad (b) \enspace \Longleftrightarrow \enspace \textcolor{rgb(73 174 65)}{10} = 25 - \textcolor{rgb(225 98 98)}{15} \times 1 \qquad (R_1') $$Injecting \( (R_1') \) into \( (R_2) \), we get:
$$ \Biggl \{ \begin{gather*} \textcolor{rgb(73 174 65)}{5} = 15 - \hspace{0.1em} \underline{ \textcolor{rgb(225 98 98)}{10} } \hspace{0.1em} \times 1 \qquad (R_2) \\ \hspace{0.1em} \underline{ \textcolor{rgb(73 174 65)}{10} } \hspace{0.1em} = 25 - \textcolor{rgb(225 98 98)}{15} \times 1 \qquad (R_1') \end{gather*} \enspace \Longrightarrow \enspace \textcolor{rgb(73 174 65)}{5} = 15 - ( 25 - \textcolor{rgb(225 98 98)}{15} \times 1 ) \times 1 \qquad (R_2') $$Once again,
$$ 1365 = \textcolor{rgb(225 98 98)}{25} \times 54 + \textcolor{rgb(73 174 65)}{15} \qquad (a) \enspace \Longleftrightarrow \enspace \textcolor{rgb(73 174 65)}{15} = 1365 - \textcolor{rgb(225 98 98)}{25} \times 54 \qquad (R_0'') $$Now injecting twice \( (R_0'') \) into \( (R_2') \), we get:
$$ \Biggl \{ \begin{gather*} \hspace{0.1em} \underline{ \textcolor{rgb(73 174 65)}{15} } \hspace{0.1em} = 1365 - \textcolor{rgb(225 98 98)}{25} \times 54 \qquad (R_0'') \\ \textcolor{rgb(73 174 65)}{5} = \hspace{0.1em} \underline{ 15 } \hspace{0.1em} - ( 25 - \hspace{0.1em} \underline{ \textcolor{rgb(225 98 98)}{15} } \hspace{0.1em} \times 1 ) \times 1 \qquad (R_2') \end{gather*} \enspace \Longrightarrow \enspace \textcolor{rgb(73 174 65)}{5} = 1365 - \textcolor{rgb(225 98 98)}{25} \times 54 - ( 25 - ( 1365 - \textcolor{rgb(225 98 98)}{25} \times 54 ) \times 1 ) \times 1 \qquad (R_2'') $$So,
$$ \textcolor{rgb(73 174 65)}{5} = 1365 - \textcolor{rgb(225 98 98)}{25} \times 54 - 25 + 1365 - \textcolor{rgb(225 98 98)}{25} \times 54 \qquad (R_2''') $$$$ \textcolor{rgb(73 174 65)}{5} = 1365 \times 2 + \textcolor{rgb(225 98 98)}{25} \times (-54 - 54 -1) $$$$ \textcolor{rgb(73 174 65)}{5} = 1365 \times 2 + \textcolor{rgb(225 98 98)}{25} \times (-109) $$We definitely have:
$$ 5 = 1365 \wedge 25 \hspace{0.2em} \Longrightarrow \hspace{0.2em} \exists (u, v) \in \hspace{0.04em}\mathbb{Z}^2, \enspace 1365u + 25v = 5 $$$$ \text{with } \Biggl \{ \begin{gather*} u = 2 \\ v = -109 \end{gather*} $$
Back to top