Convexity of a function

We call the convexity of a function \(f\) its general shape, rather bowl-shaped (convex) or rather cellar-shaped (concave).

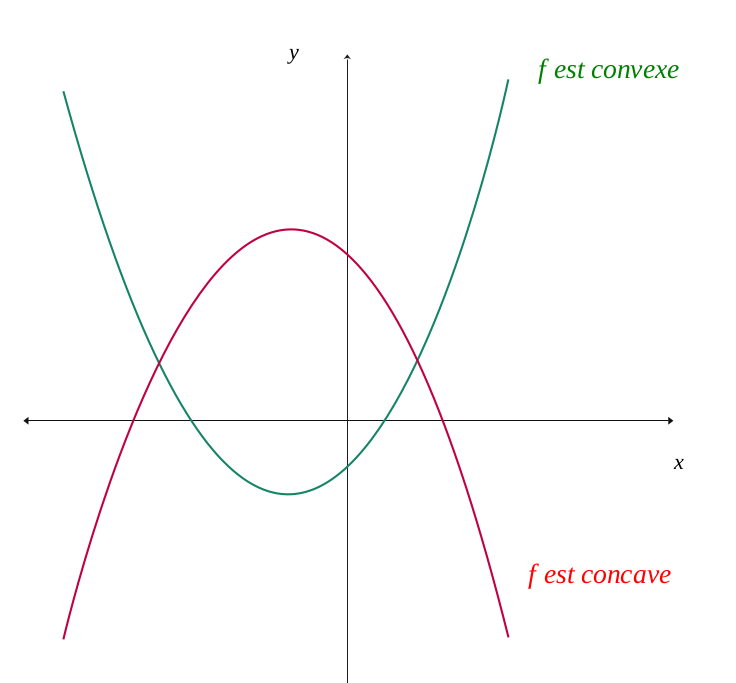
We define it more precisely according to the position of its tangents and the chords of the function.

Let \(f\) be a function of class \( \mathbb{C}^{2}\) on its definition set \( D_f \) and any interval \(I\).

The sign of the second derivative indicates convexity

Just as the derivative indicates the direction of variation of a function, the sign of the second derivative indicates convexity.

And,

The inequality of tangents

A function \( f \) is said to be convex on an interval \( I \), if any tangent at a point lies below the curve. A contrario, it is concave if any tangent is located above the curve.

The inequality of convexity

A function \( f \) is said to be convex on an interval \( I \), if any rope which connects two points of this interval lies above the curve. A contrario, it is concave if any rope is located below the curve.

---

Demonstrations

The sign of the second derivative indicates convexity

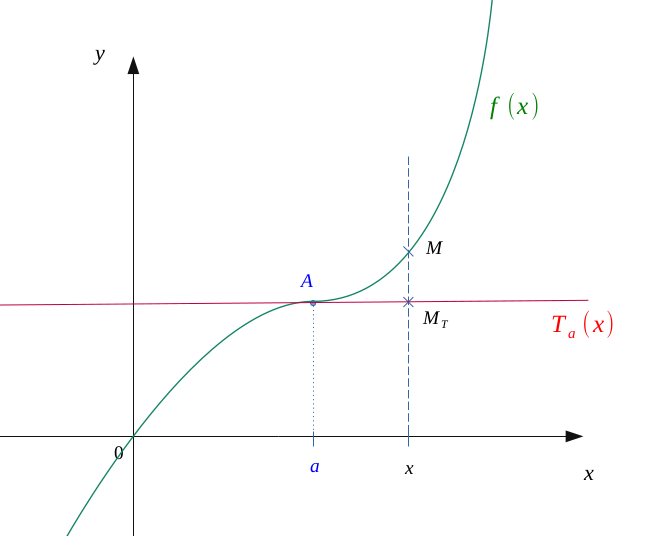
Let \(f\) be a function of class \( \mathbb{C}^{2}\) on its definition set and its tangent at a fixed point \(a\).

Let us seek to determine hte position of its tangent according to the nature of \(f\).

Let be two mobile points \(M(x;\ f(x))\) and \(M_T(x; \ T_a(x))\) depending on \(x\), respective images of \(f\) and the one of \(T_a\) at point \(x\).

The tangent equation \(T_a\) is worth:

So, point \(M_T\) will have the coordinates:

Let us now consider a new function \(g\), being worth the difference between \(f\) and \(T_a\):

To determine which of the two is above the other one, we must study the sign of \(g\) at the neighborhood of \((x=a)\), value for which the function g vanishes.

Function \(f\) being derivable twice by hypothesis and \(T_a\) being of class \( \mathbb{C}^{\infty}\), function \(g\) is also derivable twice, and:

$$ \Biggl \{ \begin{gather*} g'(x) = f'(x) - f'(a) \qquad(g') \\ g''(x) = f''(x) \hspace{5.2em}(g'') \end{gather*} $$

With \((g)\), \((g')\) and \((g''')\), we then have:

$$ (1) \ \Biggl \{ \begin{gather*} g(a) = 0 \\ g'(a) = 0 \\ g''(a) = 0 \ \Longleftrightarrow \ f''(a) = 0 \end{gather*} $$

1. Assumption of \( f''(x) > 0\) to the left and right of \(a\)

Let us assume that it is possible to find a positive number \(\eta\) such as:

$$ 0 < |x-a| < \eta \Longrightarrow f''(x) > 0 \qquad(S_+) $$

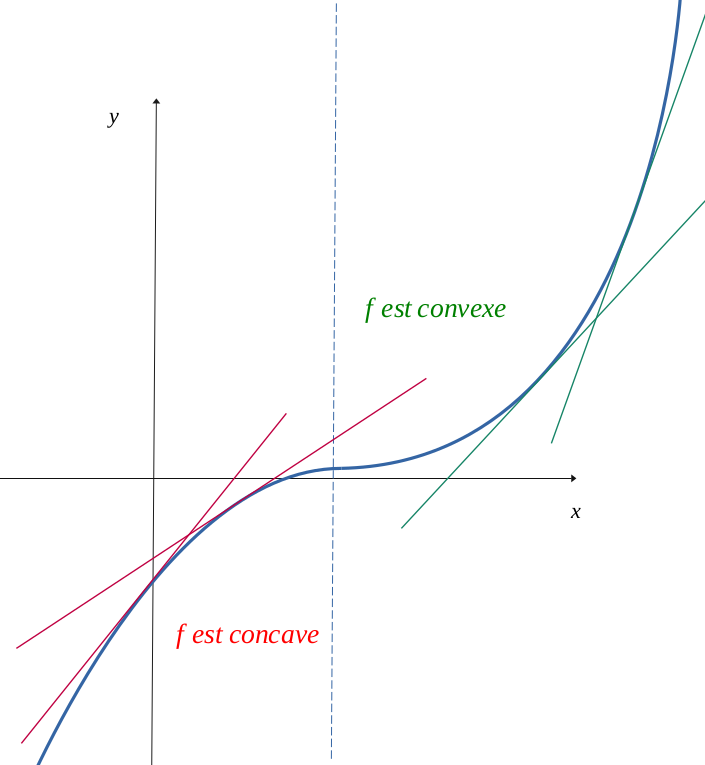
Which means that \(f''\) is supposed to be positive for the values to the left and right of \(a\). Except for \(x=a\), as clearly indicated \((S_+)\) because there may be cases where \(f''(a)\) will be infinite or even not defined at all.

This assumption made, we see with \((g'')\) that, this also entails \(g'' > 0\) to the left and right of \(a\) with \(g''(a) = 0\).

Then the derivative \(g'\) will be increasing to the left and right of \(a\), with \(g'(a) = 0\).

We will then have to the left and right of \(a\):

$$ \Biggl \{ \begin{gather*} \Bigl[ \ x < a \ \Longleftrightarrow \ g'(x) < 0 \ \Bigr] \ \Longleftrightarrow \ g \ decreasing \ for \ (x < a) \\ \Bigl[ \ x > a \ \Longleftrightarrow \ g'(x) > 0 \ \Bigr] \ \Longleftrightarrow \ g \ increasing \ for \ (x > a) \end{gather*} $$



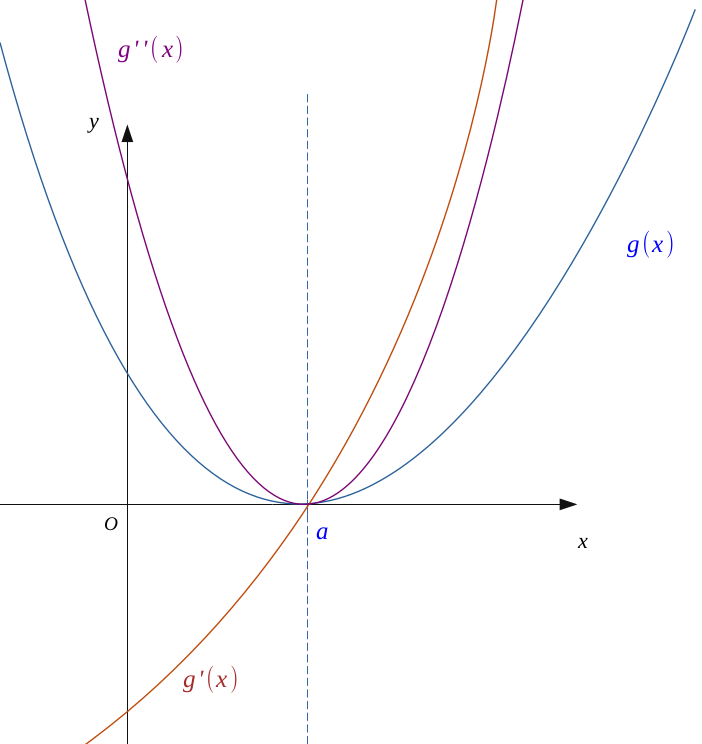
Which leads to \(g\) is decreasing on the left and increasing on the right of \(a\).

But \( g(a) = 0\), so \(g > 0\) left and right in the vicinity of \(a\).




We can conclude that for any interval \(I \):

$$ \forall x \in I, \ f''(x) \geqslant 0 \ \Longleftrightarrow f \ convex \ on \ I $$


2. Assumption of \( f''(x) < 0\) to the left and right of \(a\)

It is possible to make the same demonstration by making the opposite supposition of \((S_+)\), namely:

$$ 0 < |x-a| < \eta \Longrightarrow f''(x) < 0 \qquad (S_-) $$

So in this case \(g\) will be increasing to the left and decreasing to the right of \(a\), and we will have in the same way \(g < 0\) left and right in the vicinity of \(a\).

$$ \forall x \in I, \ f''(x) \leqslant 0 \ \Longleftrightarrow f \ concave \ on \ I $$


3. Assumption of a different sign for \( f''(x)\) to the left and right of \(a\)

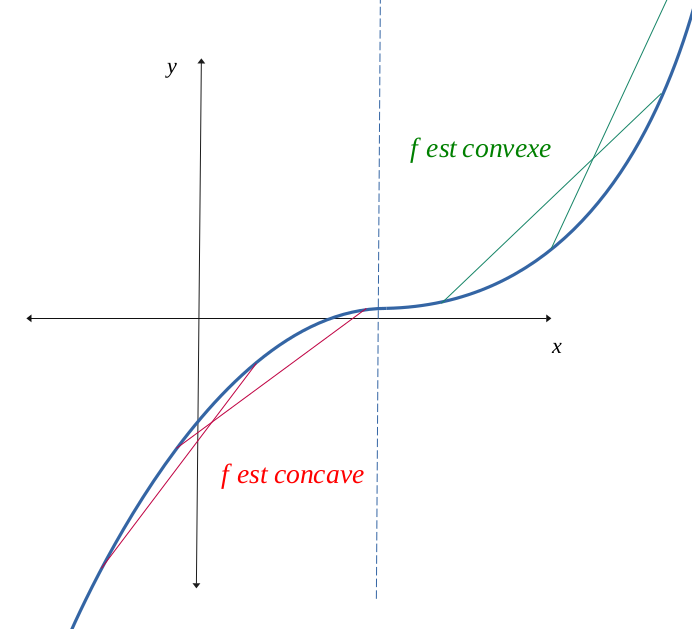
In the case where \( f''\) would have a different sign to the right and left of \(a\), there are then two cases.

Let us assume a first case, namely that \( f'' < 0\) to the left and \( f'' > 0\) on the right of \(a\). Then,

$$g''(a) = g'(a) = g(a) = 0 $$


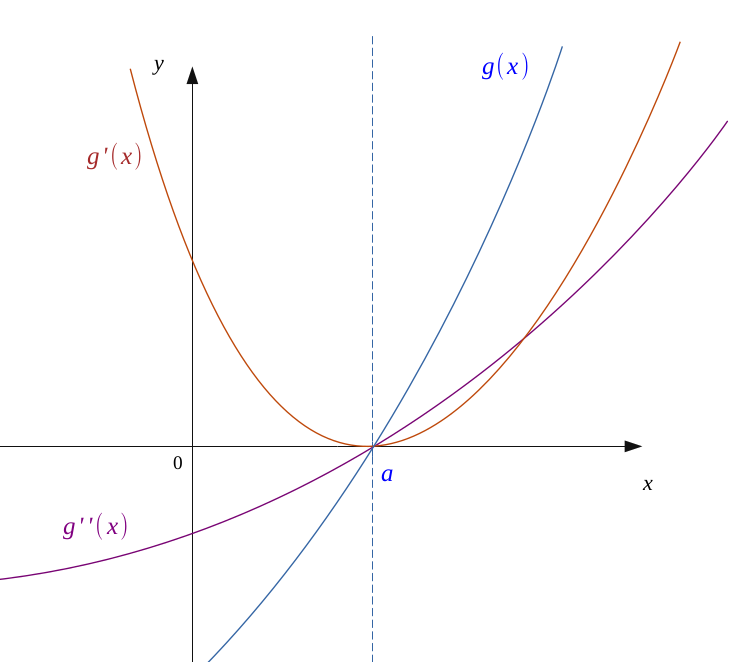
\(g'\) will be decreasing on the left then increasing on the right, which results in \(g'(x) > 0\).

So \(g\) will always be increasing and as \(g(a) = 0\), we will have \(g < 0\) to the left and \(g > 0\) on the right of \(a\).

We will then have an inflection point at point \(a\); which means \(f\) will change convexity.


$$f''(x) \ changes \ sign \ before \ and \ after \ (x=a) \Longleftrightarrow f \ admits \ an \ inflection \ point \ at \ (x=a)$$

The inequality of tangents

As we have just shown previously that if the function \(f\) is convex, then the curve of the function is always above its tangents, i.e.:

Then,

The inequality of convexity

Let \( f \) be a continuous and convex function on an interval \( I = [a,b] \), and a point \( c \in [a,b] \) of this interval, such as the following figure:

We introduce a real number \(\lambda\), proportion between points \( c \) and \( b \) according to the interval \( [a,b] \):

Consequently, we will have the other part which will be equal to:

In the following figure, we introduce a rope going from \( a \) to \( b\):

We will be able to locate the position of the rope in relation to the curve of \( f \) at point \( c \).

We then have:

1. For the curve of \( f \)

With the equation \( (\lambda)\), we do have:

$$ \lambda = \frac{b-c}{b-a} \qquad (\lambda) $$

By performing a cross product:

$$ \lambda (b-a) = b-c $$
$$ c = b - \lambda (b-a) $$
$$ c = b - \lambda b + \lambda a $$
$$ c = \lambda a + (1 - \lambda) b $$

Therefore, \( f(c) \) is worth:

$$ f(c) = f\bigl (\lambda a + (1 - \lambda) b \bigr )$$
2. For the rope going from \( a \) to \( b\)

By calculating the slope of the rope:

$$ \frac{f(b) - f(a)}{b-a} = \frac{y_c - f(a)}{c-a} $$
$$ (c-a) \frac{f(b) - f(a)}{b-a} = y_c - f(a) $$

But:

$$ 1 - \lambda = \frac{c-a}{b-a} \qquad (1 - \lambda)$$

So, replacing it by its value:

$$ (1 - \lambda) (f(b) - f(a)) = y_c - f(a) $$
$$ f(b) -f(a) - \lambda f(b) + \lambda f(a) = y_c - f(a) $$
$$ y_c = f(b) - \lambda f(b) + \lambda f(a) $$
$$ y_c = \lambda f(a) + (1 - \lambda) f(b) $$

If the function \( f \) is convex, this means that for any point \( c \in [a, b] \), its image will always be below the point of the rope \(y_c\).

And finally,

We will say that \( f \) is concave if \( (-f) \) is convexe. Thus:

By multiplying both parts by \( -1 \):

---

Examples

The inequality of convexity

Let's determine the convexity of the function \( f : x \longmapsto x^2 \) inside the interval \( [-1,1] \).

We will determine if there is any interval \( \lambda \in [0,1] \) which verifies one or the other convexity inequality.

• Side of the curve of \( f \)

We calculate in the interval \( [a, b] = [-1,1] \):

$$ g(\lambda) = f\bigl(\lambda a + (1- \lambda)b\bigr) $$

So,

$$ g(\lambda) = (-\lambda + (1- \lambda))^2 = \lambda -2\lambda(1- \lambda) + (1- \lambda)^2 $$
$$g(\lambda) = \lambda -2\lambda + 2\lambda ^2 + 1 -2\lambda + \lambda ^2$$
$$ g(\lambda) =3\lambda^2 - 3\lambda+ 1 $$
• Side of the rope between \( -1 \) and \( 1 \)

We calculate in the interval \( [a, b] = [-1,1] \):

$$ h(\lambda) = \lambda f(a) + (1 - \lambda)f(b) $$

So,

$$ h(\lambda) = \lambda (-1)^2 + (1- \lambda) 1^2 = \lambda + 1 -\lambda $$
$$ h(\lambda) = 1 $$
• Comparison of \( g(\lambda) \) with \( h(\lambda)\)

To determine the relative position of these two functions, let's take their difference.

$$ (g-h)(\lambda) = 3\lambda^2 - 3\lambda+ 1 - 1 $$
$$ (g-h)(\lambda) = 3\lambda^2 - 3\lambda $$
$$ (g-h)(\lambda) = 3\lambda (\lambda -1) $$

We can directly make a table of signs.

$$ \lambda $$	$$ -\infty $$	$$ \hspace{3em}$$	$$ 0 $$	$$ \hspace{3em}$$	$$1$$	$$ \hspace{3em}$$	$$ +\infty $$
$$ 3 \lambda $$	$$ - $$	$$ - $$	$$ 0 $$	$$ + $$	$$ + $$	$$ + $$	$$ + $$
$$ \lambda - 1$$	$$ - $$	$$ - $$	$$ - $$	$$ - $$	$$ 0 $$	$$ + $$	$$ - $$
$$ (g-h)(\lambda) $$	$$ + $$	$$ + $$	$$0 $$	$$ - $$	$$ 0 $$	$$ + $$	$$ -$$

We definitely have for all \( \lambda \in [0, 1], \enspace (g-h)(\lambda) \leqslant 0\).

It means that:

$$ g(\lambda) \leqslant f(\lambda) \Longleftrightarrow \bigl[point \enspace de \enspace la \enspace courbe\bigr] \leqslant \bigl[point \enspace de \enspace la \enspace corde \bigr] $$

The ropes are above the curve, the function is convex.