The calculation of Pi \( (\pi) \) by geometrical method

Let us calculate the value of \(\pi \) using a geometrical method.

To do this, we will process by successive iterations.

The number \(\pi \) corresponds to the ration between the half-perimeter of a circle having as radius \( R = 1 \).

The theoretical formula that we will proove is:

$$ \pi = lim_{n \to +\infty} \enspace 2^{n + 1} \sqrt{2 - \underbrace{ \sqrt{2 + \sqrt{2 + \sqrt{2 + \sqrt{2...}}} }} _\text{n} } $$ (with \( n\) the number of \( 2\) inside the second square root)

Demonstration

As we said, we will carry out several successive iterations to find this formula.

1. First approximation: by the inner square

We have represented a square of radius \( R = 1 \), as well as its internal square.



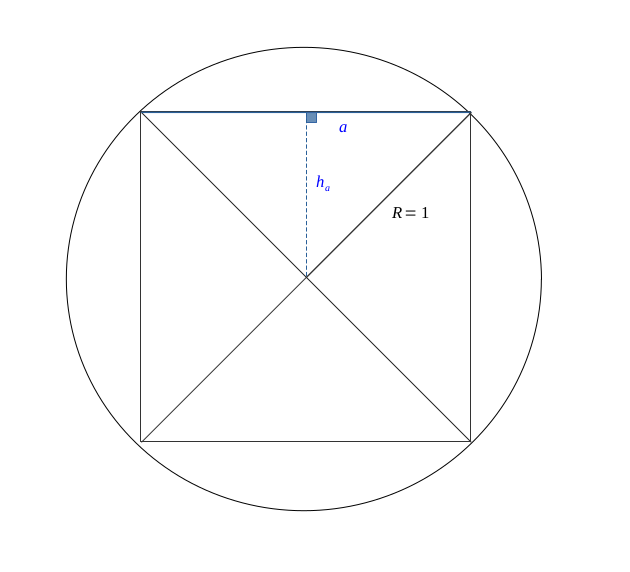
We will assume that:

$$ \pi \approx 2a $$

which is a rough first approxiamtion.

Let us calculate the value of \( a \).




With the Pythagorean theorem, we do have:

$$ a^2 = 1^2 + 1^2 $$
$$ a = \sqrt{2} \qquad(a)$$

Which gives us a first approximative value of \(\pi \):

$$ \pi \approx 2a $$
$$ \pi \approx 2\sqrt{2} $$
$$ \pi \approx 2,82 $$



2. Second approximation: by the base of the first isosceles triangle

For this second approxiamtion, we will choose a length which is closer to the circle, and we have represented it in red..

It is the base of the isosceles triangle having as one of the equal lengths, the half-diagonal of the internal square.



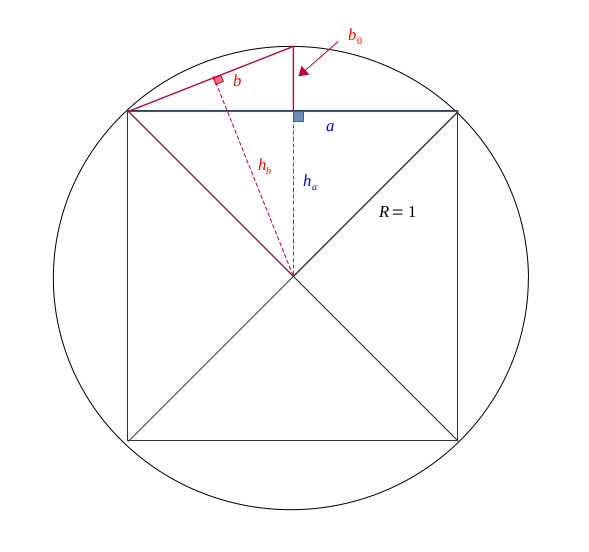
To approximate the value of \(\pi \) following the half-perimeter, this time we will need four times this length. So:

$$ \pi \approx 4b $$

Still using the Pythagorean theorem, we calculate \( b \):

$$ b^2 = \left(\frac{a}{2}\right)^2 + b_0^2 $$
$$ b^2 = \frac{a^2}{4} + (1 - h_a)^2 $$
$$ b^2 = \frac{a^2}{4} + \left(1 - \frac{a}{2}\right)^2 $$
$$ b^2 = \frac{a^2}{2} + 1 - a $$

We found out that \( a \) is worth:

$$ a = \sqrt{2} \qquad(a)$$

So:

$$ b = \sqrt{2 - \sqrt{2}} \qquad(b)$$

Which gives us that:

$$ \pi \approx 4b $$
$$ \pi \approx 4\sqrt{2 - \sqrt{2}} $$
$$ \pi \approx 3,06 $$

We see that we are starting to solwly approach \( \pi = 3,14 \dots \)




3. Third approximation: by the base of the second isosceles triangle

Let us continue the same approach with a length with always shrinks a little ore to stick the circle.


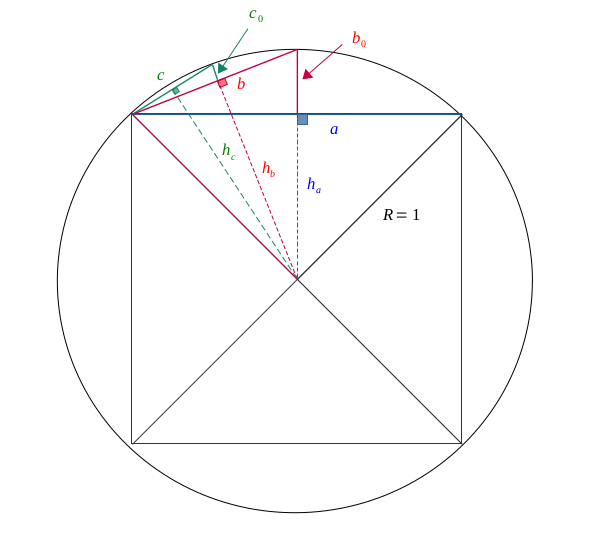
$$ \pi \approx 8c $$

We do have:

$$ c^2 = \left(\frac{b}{2}\right)^2 + c_0^2 $$
$$ c^2 = \frac{b^2}{4} + (1 - h_b)^2 $$

Here, we need to first calculate \( h_b \) :

$$ R^2 = h_b^2 + \left(\frac{b}{2}\right)^2 $$

$$ h_b^2 = R^2 - \left(\frac{b}{2}\right)^2 $$

Above, we found out that \( b = 2 - \sqrt{2}\), then:

$$ h_b^2 = 1^2 - \left(\frac{2 - \sqrt{2}}{4}\right) $$

$$ h_b^2 = 1 - \frac{1}{2} + \frac{\sqrt{2}}{4} $$

$$ h_b = \sqrt{\frac{1}{2} + \frac{\sqrt{2}}{4}} $$

$$ h_b = \frac{1}{2} \sqrt{2 + \sqrt{2}} $$

Now let us replace \( h_b \) by its value, we had:

$$ c^2 = \frac{b^2}{4} + (1 - h_b)^2 $$

So :

$$ c^2 = \frac{b^2}{4} + \left(1 - \frac{1}{2} \sqrt{2 + \sqrt{2}} \right)^2 $$

We had found for the value of \( b \):

$$ b = \sqrt{2 - \sqrt{2}} \qquad(b)$$

Hence,

$$ c^2 = \frac{2 - \sqrt{2}}{4} + 1 - 2 \times \frac{1}{2} (2 + \sqrt{2}) + \frac{2 + \sqrt{2}}{4} $$
$$ c = \sqrt{2 - \sqrt{2 + \sqrt{2 }} } \qquad(c)$$

Which gives us:

$$ \pi \approx 8c $$
$$ \pi \approx 8\sqrt{2 - \sqrt{2+ \sqrt{2 }} } $$
$$ \pi \approx 3,12 $$



4. Fourth approximation: by the base of the third isosceles triangle

Let us now continue with a new length \( d \), (too small to be drawn), found by the same process as for \( b \) and \( c \).

$$ \pi \approx 16d $$

We do have:

$$ d^2 = \left(\frac{c}{2}\right)^2 + d_0^2 $$
$$ d^2 = \frac{c^2}{4} + (1 - h_c)^2 $$

Here, we need to first calculate \( h_c \):

$$ R^2 = h_c^2 + \left(\frac{c}{2}\right)^2 $$

$$ h_c^2 = R^2 - \left(\frac{c}{2}\right)^2 $$

We have found that \( c = \sqrt{2 - \sqrt{2+ \sqrt{2 }} } \), so:

$$ h_c^2 = 1^2 - \left(\frac{2 - \sqrt{2+ \sqrt{2 }} }{4}\right) $$

$$ h_c = 1 - \frac{1}{2} + \frac{\sqrt{2+ \sqrt{2}}}{4} $$

$$ h_c = \frac{1}{2} \sqrt{2 + \sqrt{2 + \sqrt{2}}} $$

Now let us replace \( h_c \) by its value, we had:

$$ d^2 = \frac{c^2}{4} + (1 - h_c)^2 $$

So:

$$ d^2 = \frac{c^2}{4} + \left(1 - \frac{1}{2} \sqrt{2 + \sqrt{2 + \sqrt{2}}} \right)^2 $$

We had hound for the value of \( c \):

$$ c = \sqrt{2 - \sqrt{2 + \sqrt{2 }} } \qquad(c)$$

Hence,

$$ d^2 = \frac{ \sqrt{2 - \sqrt{2+ \sqrt{2 }} }}{4} + 1 - 2 \times \frac{1}{2} \sqrt{2 + \sqrt{2 + \sqrt{2}}} + \frac{2 + \sqrt{2 + \sqrt{2}}}{4} $$
$$ d = \sqrt { 2 - \sqrt { 2 + \sqrt { 2 + \sqrt{2}}} } \qquad(d)$$

Which gives us:

$$ \pi \approx 16d $$
$$ \pi \approx 16\sqrt { 2 - \sqrt { 2 + \sqrt { 2+ \sqrt{2}}} } $$
$$ \pi \approx 3,13 $$

By repeating the same process endlessly, we end with a generalization.




5. Generalization

Let us recap.

We found these different values ​​for \( \pi \):

$$ \pi \approx 2\sqrt{2} \qquad (n = 0) $$
$$ \pi \approx 4\sqrt{2 - \sqrt{2}} \qquad (n = 1) $$
$$ \pi \approx 8\sqrt{2 - \sqrt{2+ \sqrt{2 }} } \qquad (n = 2) $$
$$ \pi \approx 16\sqrt { 2 - \sqrt { 2 + \sqrt { 2+ \sqrt{2}}} } \qquad (n = 3) $$

We see clearly that it is then possible to generalize this value, by making \( n \to \infty \).

And as a result,

$$ \pi = lim_{n \to +\infty} \enspace 2^{n + 1} \sqrt{2 - \underbrace{ \sqrt{2 + \sqrt{2 + \sqrt{2 + \sqrt{2...}}} }} _\text{n} } $$ (with \( n\) the number of \( 2\) inside the second square root)